Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-15T03:48:07.215Z Has data issue: false hasContentIssue false
  • English
  • Français

An Extremal Problem in Number Theory

Published online by Cambridge University Press:  20 November 2018

H. L. Abbott  and
B. Gardner
H. L. Abbott
Affiliation:
Memorial University of Newfoundland
B. Gardner
Affiliation:
Memorial University of Newfoundland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

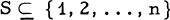Let n and k be integers with n ≥ k ≥ 3. Denote by f(n, k) the largest positive integer for which there exists a set S of f (n, k) integers satisfying (i) and (ii) no k members of S have pairwise the same greatest common divisor. The problem of determining f(n, k) appears to be difficult. Erdős [2[ proved that there is an absolute constant c > 1 such that for every ∈ > 0 and every fixed k

1

provided n > no (k, ∈). In [l[ it i s proved that for every ∈ > 0 and every fixed k

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 10 , Issue 2 , June 1967 , pp. 173 - 177
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Abbott, H. L., Some remarks on a combinatorial theorem of Erdős and Rado. Can. Math. Bull. vol. 9, no. 2 (1966) pages 155-160.Google Scholar
2. Erdős, P., On à problem in elementary number theory and a combinatorial problem. Math, of Comp.. vol. 18, no. 8. (1966), pages 644-646.Google Scholar