Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beck, Eugen
1977.
�ber Mittelwerte aus Potenzproduktsummen.
Monatshefte f�r Mathematik,
Vol. 83,
Issue. 3,
p.
177.
Mokkadem, Abdelkader
Mokkadem, Abdelkader
Pelletier, Mariane
Pelletier, Mariane
Worms, Julien
and
Worms, Julien
2005.
A large deviations upper bound for the kernel mode estimator.
Теория вероятностей и ее применения,
Vol. 50,
Issue. 1,
p.
189.


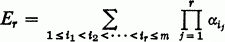

 denote the binomial coefficient. If α
denote the binomial coefficient. If α