Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-26T06:27:03.022Z Has data issue: false hasContentIssue false
  • English
  • Français

An Upper Limit Property of the Euler Function

Published online by Cambridge University Press:  20 November 2018

Miriam Hausman
Miriam Hausman*
Affiliation:
Department of Mathematics Baruch College 17 Lexington Ave., New York, N.Y. 10010
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If ϕ(n) denotes the Euler function, for n = p a prime we have ϕ(n)/n = (1-1/p), which implies that

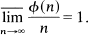
In this note we consider a refinement of this result. Namely, we prove that

1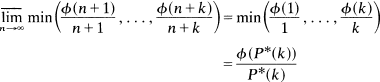

where P∗(k) is the largest integer of the form 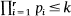where p1 < p2<…<pr are the first r primes in ascending order.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 3 , 01 September 1980 , pp. 375 - 377
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Hardy, G. H., and Wright, E. M., An Introduction to the Theory of Numbers, Oxford University Press, 1968, p. 351.Google Scholar