Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T21:23:04.453Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Existence of Resolvable Graph Designs

Published online by Cambridge University Press:  20 November 2018

Peter Dukes  and
Alan C. H. Ling
Peter Dukes
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria, BC, V8W 3P4 e-mail: dukes@math.uvic.ca
Alan C. H. Ling
Affiliation:
Department of Computer Science, University of Vermont, Burlington, VT 05405, U.s.A. e-mail: aling@emba.uvm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 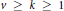$v\,\ge \,k\,\ge \,1$ and 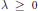$\lambda \,\ge \,0$ be integers. A block design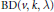$\text{BD}\left( v,\,k,\,\lambda \right)$ is a collection 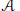$\mathcal{A}$ of $k$-subsets of a $v$-set 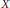$X$ in which every unordered pair of elements from 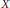$X$ is contained in exactly $\lambda $ elements of 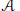$\mathcal{A}$. 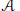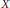More generally, for a fixed simple graph $G$, a graph design$\text{GD}\left( v,\,G,\,\lambda \right)$ is a collection $\mathcal{A}$ of graphs isomorphic to $G$ with vertices in $X$ such that every unordered pair of elements from 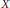$X$ is an edge of exactly $\lambda $ elements of 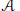$\mathcal{A}$. A famous result of Wilson says that for a fixed $ $ and $\lambda $, there exists a $\text{GD}\left( v,\,G,\,\lambda \right)$ for all sufficiently large $ $ satisfying certain necessary conditions. A block (graph) design as above is resolvable if 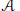$\mathcal{A}$ can be partitioned into partitions of (graphs whose vertex sets partition) 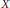$X$. 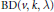Lu has shown asymptotic existence in $v$ of resolvable $\text{BD}\left( v,\,k,\,\lambda \right)$, yet for over twenty years the analogous problem for resolvable $\text{GD}\left( v,\,G,\,\lambda \right)$ has remained open. In this paper, we settle asymptotic existence of resolvable graph designs.

Keywords

05B0505C7005B10graph decompositionresolvable designs
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 504 - 518
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Adams, P., Bryant, D. E., and Khodkar, A., The spectrum problem for λ-fold Petersen graph designs. J. Combin. Math. Combin. Comput. 34(2000), 159–176.Google Scholar
[2] Chowla, S., Erdős, P., and Strauss, E. G., On the maximal number of pairwise orthogonal Latin squres of a given order. Canad. J. Math. 12(1960), 204–208.Google Scholar
[3] Furino, S., Miao, Y., and Yin, J., Frames and Resolvable Designs. Uses, Constructions, and Existence. CRC Press, Boca Raton, FL, 1996.Google Scholar
[4] Lamken, E. R. and Wilson, R. M., Decompositions of edge-colored complete graphs. J. Combin. Theory Ser. A 89(2000), no. 2, 149–200.Google Scholar
[5] Lu, J. X., An existence theory for resolvable balanced incomplete block designs. (Chinese) Acta Math. Sinica 27(1984), no. 4, 458–468.Google Scholar
[6] Ray-Chaudhuri, D. K. and Wilson, R. M., The existence of resolvable block designs. In: Survey of Combinatorial Theory. North-Holland, Amsterdam, 1971, pp. 361–375.Google Scholar
[7] Rees, R., Two new direct product-type constructions for resolvable group-divisible designs. J. Combin. Des. 1(1993), no. 1, 15–26.Google Scholar
[8] Schrijver, A., Theory of Linear and Integer Programming. John Wiley & Sons, Chichester, 1986.Google Scholar
[9] Wilson, R. M., Cyclotomy and difference families in elementary abelian groups. J. Number Theory 4(1972), 17–47.Google Scholar
[10] Wilson, R. M., Decompositions of complete graphs into subgraphs isomorphic to a given graph. In: Congressus Numerantium XV, Utilitas Math. Winnipeg, MB. 1976, pp. 647–659.Google Scholar
[11] Wilson, R. M. The necessary conditions for t-designs are sufficient for something. Congressus Numerantium IV, Utilitas Math. Winnipeg, MB. 1973, pp. 207–215.Google Scholar