Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T04:48:27.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Existence of Tight Orthogonal Main Effect Plans

Published online by Cambridge University Press:  20 November 2018

Robert Gallant  and
Charles J. Colbourn
Robert Gallant
Affiliation:
Department of Combinatorics and Optimization University of Waterloo Waterloo, Ontario N2L 3G1
Charles J. Colbourn
Affiliation:
Department of Combinatorics and Optimization University of Waterloo Waterloo, Ontario N2L 3G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our main result is showing the asymptotic existence of tight 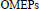$\text{OMEPs}$. More precisely, for each fixed number 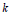$k$ of rows, and with the exception of 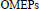$\text{OMEPs}$ of the form 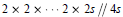$2\times 2\times \cdot \cdot \cdot 2\times 2s\,//\,4s\,\,$ with 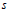$s$ odd and with more than three rows, there are only a finite number of tight $\text{OMEP}$ parameters for which the tight $\text{OMEP}$ does not exist.

Keywords

62K9905B15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 1 , 01 March 1998 , pp. 33 - 40
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Addelman, S., Orthogonal Main-Effect Plans for Asymmetrical Factorial Experiments. Technometrics 4 (1962), 21–46.Google Scholar
2. Beth, Th., Jungnickel, D. and Lenz, H., Design Theory. Bibliographisches Institut, Mannheim, Germany, 1985.Google Scholar
3. Jacroux, M., A Note on the Determination and Construction of Minimal Orthogonal Main-Effect Plans. Technometrics 34(1992) 92–96.Google Scholar
4. Gallant, R. P. and Colbourn, C. J., Tight Four Factor Orthogonal Main Effect Plans. Discrete Math., to appear.Google Scholar
5. Street, D. J., Constructions for Orthogonal Main Effect Plans. Utilitas Math. 45 (1994), 115–123.Google Scholar
6. Street, D. J. and Burgess, L., A Survey of Orthogonal Main Effect Plans and Related Structures. Congr. Numer. 99 (1994), 223–239.Google Scholar