Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T05:11:46.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Results for Class Number Divisibility in Cyclotomic Fields

Published online by Cambridge University Press:  20 November 2018

Frank Gerth III
Frank Gerth III*
Affiliation:
Department of Mathematics, The University of TexasAustin, Texas 78712, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

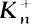Let n ≥3 and m≥3 be integers. Let Kn be the cyclotomic field obtained by adjoining a primitive nth root of unity to the field of rational numbers. Let denote the maximal real subfield of 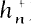Kn. Let hn (resp., ) denote the class number of 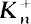Kn (resp., ). For fixed 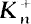m we show that m divides hn and hn for asymptotically almost all n. 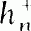Also for those Kn and with a given number of ramified primes, we obtain lower bounds for certain types of densities for m dividing hn and .

Keywords

12A3512A5012A75
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 4 , 01 December 1983 , pp. 464 - 472
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Cornell, G. and Rosen, M., The l-rank of the real class group of cyclotomic fields, Abstracts Amer. Math. Soc, 3 (1982), 226.Google Scholar
2. Cornell, G. and Washington, L., Class numbers of cyclotomic fields, to appear.Google Scholar
3. Gerth, F. and Graham, S., Counting certain number fields with l-class number 1 or I, to appear.Google Scholar
4. Gerth, F., Counting certain number fields with prescribed l-class numbers, to appear in J. Reine Angew. Math.Google Scholar
5. Halberstam, H. and Richert, H.-E., Sieve Methods, Academic Press, London, 1974.Google Scholar