Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T13:18:09.200Z Has data issue: false hasContentIssue false
  • English
  • Français

The Average Edge Order of 3-Manifold Coloured Triangulations

Published online by Cambridge University Press:  20 November 2018

Maria Rita Casali
Maria Rita Casali*
Affiliation:
Dipartimento di Matematica Pura ed Applicata, Università di Modena, Via Campi 213B, I-41100 Modena, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If K is a triangulation of a closed 3-manifold M with E0(K) edges and F0(K) triangles, then the average edge order of K is defined to be

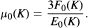
In [8], the relations between this quantity and the topology of M are investigated, especially in the case of μ0(K) being small (where the study relies on Oda's classification of triangulations of 𝕊2 up to eight vertices—see [9]). In the present paper, the attention is fixed upon the average edge order of coloured triangulations; surprisingly enough, the obtained results are perfectly analogous to Luo-Stong' ones, and may be proved with little effort by means of edge-coloured graphs representing manifolds.

Keywords

57Q1505C1057M15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 2 , 01 June 1994 , pp. 154 - 161
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Bracho, J. and Montejano, L., The combinatorics of colored triangulations of manifolds, Geom. Dedicata 22(1987), 303–328.Google Scholar
2. Ferri, M. and Gagliardi, C., Crystallization moves, Pacific J. Math. 100(1982), 233–246.Google Scholar
3. Ferri, M., Gagliardi, C. and Grasselli, L., A graph-theoretical representation of PL-manifolds. A survey on crystallizations, Aequationes Math. 31(1986), 121–141.Google Scholar
4. Gagliardi, C., Regular imbeddings of edge-coloured graphs, Geom. Dedicata 11(1981), 397–414.Google Scholar
5. Gagliardi, C., On a class of“3-dimensionalpolyhedra, Ann. Univ. Ferrara Sez. VII 33(1987), 51–88.Google Scholar
6. Hilton, P. J. and Wylie, S., An introduction to algebraic topology—Homology theory, Cambridge Univ. Press, 1960.Google Scholar
7. Lins, S. and Mandel, A., Graph-encoded 3-manifolds, Discrete Math. 57(1985), 261–284.Google Scholar
8. Luo, F. andStong, R., Combinatorics of triangulations of'h-manifolds, Trans. Amer. Math. Soc. 337(1993), 891–906.Google Scholar
9. Oda, T., Convex bodies and algebraic geometry, Springer-Verlag, 1985.Google Scholar
10. Pezzana, M., Diagrammi di Heegaarde triangolazione contratta, Boll. Un. Mat. Ital. 12(1975), 93–105.Google Scholar
11. Rourke, C. and Sanderson, B., Introduction to Piecewise-linear Topology, Springer-Verlag, 1972.Google Scholar
12. Vince, A., Combinatorial maps, J. Combin. Theory Ser. B 34(1983), 1–21.Google Scholar