Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T16:31:49.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Bernstein's Inequality in the Bivariate Case

Published online by Cambridge University Press:  20 November 2018

Kenneth Mullen
Kenneth Mullen*
Affiliation:
University of Guelph, Guelph Ontario
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

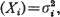If (Xl, X2,…, Xn), is a set of n independent random variables, such that EXi=0, Var and if t is a real positive number and 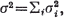, then Bernstein [2] has given an upper bound for Pr 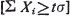when the X's are bounded. The best English language discussion of Bernstein's work is probably by Bennett [1].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 16 , Issue 1 , March 1973 , pp. 83 - 86
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Bennett, George, Probability inequalities for the sum of independent random variables, J. Amer. Statist. Assoc. 57 (1962), 33–45.Google Scholar
2. Bernstein, S., Sur une modification de V’inéqualité de Tchebichef (in Russian, French Summary), Ann. Sci. Inst. Sew. Ukraine Sect. Math. I, 1924.Google Scholar