Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T15:53:25.073Z Has data issue: false hasContentIssue false
  • English
  • Français

A Big Picard Theorem for Holomorphic Maps into Complex Projective Space

Published online by Cambridge University Press:  20 November 2018

Yasheng Ye  and
Min Ru
Yasheng Ye
Affiliation:
Department of Mathematics, University of Shanghai for Science and Technology, Shanghai 200093, P.R. China e-mail: yashengye@yahoo.com.cn
Min Ru
Affiliation:
Department of Mathematics, University of Houston, Houston, TX 77204 e-mail: minru@math.uh.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a big Picard type extension theoremfor holomorphic maps 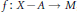$f\,:\,X\,-\,A\,\to \,M$, where $X$ is a complex manifold, 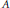$A$ is an analytic subvariety of $X$, and 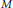$M$ is the complement of the union of a set of hyperplanes in ${{\mathbb{P}}^{n}}$ but is not necessarily hyperbolically imbedded in ${{\mathbb{P}}^{n}}$.

Keywords

32H30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 1 , 01 March 2009 , pp. 154 - 160
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Dufresnoy, J., Théorie nouvelle des familles complexes normales. Applications à l’étude des fonctions algébroïdes. Ann. Sci. École Norm. Sup. 61(1944), 1–44.Google Scholar
[2] Fujimoto, H., Extensions of the big Picard's theorem. Tôhoku Math. J. 24(1972), 415–422.Google Scholar
[3] Green, M. L., Some Picard theorems for holomorphic maps to algebraic varieties. Amer. J. Math. 97(1975), 43–75.Google Scholar
[4] Kiernan, P., Extensions of holomorphic maps. Trans. Amer. Math. Soc. 172(1972), 347–355.Google Scholar
[5] Kobayashi, K., Hyperbolic manifolds and holomorphic mappings. In: Pure and Applied Mathematics 2, Marcel Dekker, Inc., New York, 1970.Google Scholar
[6] Kwack, M. H., Generalization of the big Picard theorem. Ann. of Math. (2) 90(1969), 9–22,Google Scholar
[7] Levin, A., The dimension of integral points and holomorphic curves on the complements of hyperplanes. math.NT/0601691, http://arxiv.org/pdf/math/0601691v1.Google Scholar
[8] Ru, M., Geometric and arithmetic aspects of ℙ n minus hyperplanes. Amer. J. Math. 117(1995), no. 2, 307–321.Google Scholar