Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-11T02:43:19.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Block Sizes in Pairwise Balanced Designs

Published online by Cambridge University Press:  20 November 2018

Charles J. Colbourn ,
Kevin T. Phelps  and
Vojtěch Rödl
Charles J. Colbourn
Affiliation:
Department of Computational Science, University of Saskatchewan, Saskatoon, Saskatchewan S7N 0W0, Canada
Kevin T. Phelps
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, Georgia 30332, U.S.A.
Vojtěch Rödl
Affiliation:
FJFI, CVUT, Husova 5, Praha 1, Czechoslovakia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

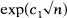The number of sets of integers which are realizable as block sizes of a pairwise balanced design of order n is between and 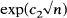; in contrast, when the multiplicity of each block size is also specified, the number of multisets which can be realized is between 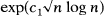and 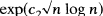. Although this gives a reasonable bound on the number of multisets which can be realized, a good characterization is not likely to exist; deciding whether a multiset can be so realized is NP-complete.

Keywords

05B3005B05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 3 , 01 September 1984 , pp. 375 - 380
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Erdös, P., Problems and Results on Block Designs and Set Systems, Proceedings of the Thirteenth Southeastern Conference on Combinatorics, Graph Theory, and Computing, 1982, pp. 3–18.Google Scholar
2. Erdös, P. and Gallai, T., Graphs with prescribed degrees of vertices (Hungarian), Mat. Lapok 11 (1960), 264–274.Google Scholar
3. Garey, M. R. and Johnson, D. S., Computers and Intractability, Freeman and Sons, San Francisco, CA, 1979.Google Scholar
4. Hall, J. I., Bounds for equidistant codes and partial projective planes, Discrete Mathematics 17 (1977), 85–94.Google Scholar
5. Vanstone, S. A., The extendibility of (r, 1) designs, Proceedings of the Third Manitoba Conference on Numerical Mathematics and Computing, 1973.Google Scholar