Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T05:31:47.076Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bockstein Map is Necessary

Published online by Cambridge University Press:  20 November 2018

Marius Dădărlat  and
Søren Eilers
Marius Dădărlat
Affiliation:
Department of Mathematics Purdue University West Lafayette, Indiana 47907 U.S.A., email: mdd@math.purdue.edu
Søren Eilers
Affiliation:
Matematisk Afdeling KØbenhavns Universitet Universitetsparken 5 DK-2100 Copenhagen Ø Denmark, email: eilers@math.ku.dk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct two non-isomorphic nuclear, stably finite, real rank zero 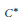${{C}^{*}}$-algebras 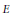$E$ and 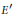${{E}^{'}}$ for which there is an isomorphism of ordered groups 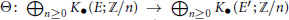$\Theta :{{\oplus }_{n\ge 0}}{{K}_{\bullet }}(E;\mathbb{Z}/n)\to {{\oplus }_{n\ge 0}}{{K}_{\bullet }}({E}';\mathbb{Z}/n)$ which is compatible with all the coefficient transformations. The 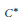${{C}^{*}}$-algebras 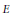$E$ and 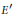${{E}^{'}}$ are not isomorphic since there is no 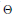$\Theta$ as above which is also compatible with the Bockstein operations. By tensoring with Cuntz’s algebra 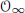${{\mathcal{O}}_{\infty }}$ one obtains a pair of non-isomorphic, real rank zero, purely infinite 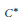${{C}^{*}}$-algebras with similar properties.

Keywords

46L3546L8019K14K-theorytorsion coefficientsnatural transformationsBockstein mapsC*-algebrasreal rank zeropurely infiniteclassification
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 3 , 01 September 1999 , pp. 274 - 284
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Dădărlat, M. and Eilers, S., Compressing coefficients while preserving ideals in the K-theory for C*-algebras. K-theory 14 (1998), 281–304.Google Scholar
[2] Dădărlat, M., Approximate homogeneity is not a local property. J. Reine Angew.Math. 507 (1999), 1–14.Google Scholar
[3] Dădărlat, M. and Gong, G., A classification result for approximately homogeneousC*-algebras of real rank zero. Geom. Funct. Anal. 7 (1997), 646–711.Google Scholar
[4] Dădărlat, M., A classification result for approximately homogeneous C*-algebras of real rank zero, II. Preprint.Google Scholar
[5] Dădărlat, M. and Loring, T. A., Extensions of certain real rank zero C*-algebras. Ann. Inst. Fourier 44 (1994), 907–925.Google Scholar
[6] Dădărlat, M., Classifying C*-algebras via ordered, mod-p K-theory. Math. Ann. 305 (1996), 601–616.Google Scholar
[7] Dădărlat, M., A universal multicoefficient theorem for the Kasparov groups. Duke Math. J. 84 (1996), 355–377.Google Scholar
[8] Dădărlat, M. and Nemethi, A., Shape theory and connective K-theory. J. Operator Theory 23 (1990), 207–291.Google Scholar
[9] Eilers, S., Invariants for AD algebras. Ph.D. thesis, Copenhagen University, 1995.Google Scholar
[10] Eilers, S., A complete invariant for AD algebras with real rank zero and bounded torsion in K1 . J. Funct. Anal. 139 (1996), 325–348.Google Scholar
[11] Elliott, G. A., On the classification ofC*-algebras of real rank zero. J. Reine Angew.Math. 443 (1993), 179–219.Google Scholar
[12] Gong, G., Classification of C*-algebras of real rank zero and unsuspended E-equivalence types. J. Funct. Anal. 152 (1998), 281–329.Google Scholar
[13] Kirchberg, E., Exact C*-algebras, tensor products, and classification of purely infinite C*-algebras. Proc. I.C.M., Zürich, 1994, 943–954, Birkhauser, Verlag, Basel.Google Scholar
[14] Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov's generalized functor. Duke Math. J. 55 (1987), 431–474.Google Scholar
[15] Schochet, C., Topological methods for C*-algebras IV: Mod p homology. Pacific J.Math. 114 (1984), 447–468.Google Scholar
[16] Zhang, S., A Riesz decomposition property and ideal structure of multiplier algebras. J. Operator Theory 24 (1990), 209–225.Google Scholar
[17] Zhang, S., A property of purely infinite simple C*-algebras. Proc. Amer.Math. Soc. 109 (1990), 717–720.Google Scholar