Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T07:29:17.413Z Has data issue: false hasContentIssue false
  • English
  • Français

Boolean Algebras and Raising Maps to Zero-Dimensional Spaces

Published online by Cambridge University Press:  20 November 2018

Jan van Mill
Jan van Mill*
Affiliation:
Subfaculteit Wlskunde, Vrije Universiteit De Boelelaan 1081 Amsterdam, The Netherlands
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a separable metric space and let 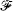be a family of countably many self-maps of X. Then there is a countable subalgebra 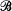of the Boolean algebra of regular open subsets of X which is a base for X such that for each 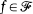the function 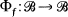defined by Φf(B) = (f-1(B))-0 is a homomorphism.

Keywords

54E4506E15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 1 , 01 March 1983 , pp. 70 - 79
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Aarts, J. M., Every metric compactification is a Wallman-type compactification, Proc. Int. Symp. on Topology and its Applications, Herceg-Novi (Yugoslavia) (1968).Google Scholar
2. Anderson, R. D., On raising flows and mappings, Bull. Amer. Math. Soc. 69 (1963) 259-264.Google Scholar
3. Baayen, P. C., Universal morphisms, Mathematical Centre Tracts 9, Amsterdam (1964).Google Scholar
4. Berney, E. S., On Wallman compactifications, Notices Am. Math. Soc. 17 (1970) 215.Google Scholar
5. Comfort, W. W. and Negrepontis, S., The theory of ultrafilters, Die Grundlehren der Math. Wissenschaften in Einzeldarstellungen, Band 211, Springer Verlag, Berlin and New York (1974).Google Scholar
6. Steiner, A. K. and Steiner, E. F., Products of compact metric spaces are regular Wallman, Indag. Math. 30 (1968) 428-430.Google Scholar