Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Borosh, I
Flahive, M
and
Treybig, B
1986.
Small solutions of linear Diophantine equations.
Discrete Mathematics,
Vol. 58,
Issue. 3,
p.
215.
O’Leary, Robbin
and
Vaaler, Jeffrey D.
1993.
Small solutions to inhomogeneous linear equations over number fields.
Transactions of the American Mathematical Society,
Vol. 336,
Issue. 2,
p.
915.
Chandrasekaran, R.
2015.
Integer Farkas Lemma.
International Game Theory Review,
Vol. 17,
Issue. 01,
p.
1540003.
Dubrulle, Paul
Kosmatov, Nikolai
Gaston, Christophe
and
Lapitre, Arnault
2021.
PolyGraph: a data flow model with frequency arithmetic.
International Journal on Software Tools for Technology Transfer,
Vol. 23,
Issue. 3,
p.
489.
Gribanov, Dmitry
Shumilov, Ivan
Malyshev, Dmitry
and
Pardalos, Panos
2024.
On $$\Delta $$-modular integer linear problems in the canonical form and equivalent problems.
Journal of Global Optimization,
Vol. 88,
Issue. 3,
p.
591.

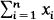 is minimal, then
is minimal, then 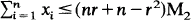 .
.