Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T01:37:09.612Z Has data issue: false hasContentIssue false
  • English
  • Français

C*-Convexity and the Numerical Range

Published online by Cambridge University Press:  20 November 2018

Bojan Magajna
Bojan Magajna*
Affiliation:
Department of Mathematics University of Ljubljana Jadranska 19 Ljubljana 1000 Slovenia, e-mail: Bojan.Magajna@fmf.uni-lj.si
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 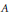$A$ is a prime 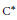${{\text{C}}^{*}}$-algebra, 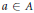$a\,\in \,A$ and 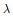$\lambda $ is in the numerical range 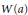$W\left( a \right)$ of 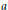$a$, then for each 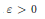$\varepsilon \,>\,0$ there exists an element 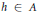$h\,\in \,A$ such that 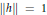$\left\| h \right\|\,=\,1$ and 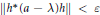$\left\| {{h}^{*}}(a-\lambda )h \right\|\,<\,\varepsilon $. If 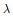$\lambda $ is an extreme point of 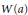$W\left( a \right)$, the same conclusion holds without the assumption that 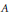$A$ is prime. Given any element $a$ in a von Neumann algebra (or in a general 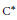${{\text{C}}^{*}}$-algebra) 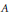$A$, all normal elements in the weak* closure (the norm closure, respectively) of the 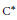${{\text{C}}^{*}}$-convex hull of $a$ are characterized.

Keywords

47A1246L0546L10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 2 , 01 June 2000 , pp. 193 - 207
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Anantharaman-Delaroche, C., Some remarks on the cone of completely positive maps between von Neumann algebras. LondonMath, J.. Soc. 55(1997), 193–208.Google Scholar
[2] Anantharaman-Delaroche, C. and Havet, J. F., Approximate factorizations of completely positivemaps. Funct, J.. Anal. 90(1990), 411–428.Google Scholar
[3] Arveson, W., Subalgebras of C*-algebras II. Acta Math. 128(1972), 271–308.Google Scholar
[4] Bonsall, F. F. and Duncan, J., Numerical ranges of operators on normed spaces and elements of normed algebras. LondonMath. Soc. Lecture Note Series 2, Cambridge Univ. Press, Cambridge, 1971.Google Scholar
[5] Bonsall, F. F. and Duncan, J., Numerical ranges II. London Math. Soc. Lecture Note Series 10, Cambridge Univ. Press, Cambridge, 1973.Google Scholar
[6] Davidson, K. R., C*-algebras by example. Fields Institute Monographs, Amer. Math. Soc., Providence, R.I., 1996.Google Scholar
[7] Dixmier, J., Les Algebres d’Opérateurs dans l’Espace Hilbertien. Gauthier-Villars, Paris, 1969.Google Scholar
[8] Elliott, G. A. and Zsido, L., Almost uniformly continuous automorphism groups of operator algebras. Operator, J. Theory 8(1982), 227–277.Google Scholar
[9] Farenick, D. R., Krein-Milman type problems for compact matricially convex sets. Linear Algebra Appl. 162– 164(1992), 325–334.Google Scholar
[10] Fillmore, P. A., Stampfli, J. G. and Williams, J. P., On the essential range, the essential spectrum and a problem of Halmos. Acta Sci. Math. (Szeged) 33(1972), 179–192.Google Scholar
[11] Glimm, J., A Stone-Weierstrass theorem for C*-algebras. Ann. of Math. 72(1960), 216–244.Google Scholar
[12] Haagerup, U. and Zsido, L., Sur la propriété de Dixmier pour les C*-algebras. R, C.. Acad. Sci. Paris, Ser. I Math. 298(1984), 173–176.Google Scholar
[13] Halpern, H., Module homomorphisms of a von Neumann algebra into its center. Trans. Amer. Math. Soc. 140(1969), 183–193.Google Scholar
[14] Halpern, H., Irreducible module homomorphisms of a von Neumann algebra into its center. Trans. Amer. Math. Soc. 140(1969), 195–221.Google Scholar
[15] Halpern, H., Essential central spectrum and range for elements of a von Neumann algebra. Pacific Math, J.. 43(1972), 349–380.Google Scholar
[16] Hiai, F. and Nakamura, Y., Closed convex hulls of unitary orbits in von Neumann algebras. Trans. Amer.Math. Soc. 323(1991), 1–38.Google Scholar
[17] Kadison, R. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras.Vols. 1, 2, Academic Press, London, 1983, 1986.Google Scholar
[18] Loebl, R. I. and Paulsen, V. I., Some remarks on C*-convexity. Linear Algebra and Appl. 35(1981), 63–78.Google Scholar
[19] Magajna, B., The Haagerup norm on the tensor product of operator modules. Funct, J.. Anal. 129(1995), 325–348.Google Scholar
[20] Magajna, B., A transitivity problem for completely bounded mappings. Houston Math, J.. 23(1997), 109–120.Google Scholar
[21] Morenz, P. B., The structure of C*-convex sets. Canad. Math, J.. 46(1994), 1007–1026.Google Scholar
[22] Paschke, W. L., Inner product modules over B*-algebras. Trans. Amer.Math. Soc. 182(1973), 443–468.Google Scholar
[23] Paulsen, V. I., Completely bounded maps and dilations. Pitman Res. Notes Math. Ser. 146, London, 1986.Google Scholar
[24] Pedersen, G. K., C*-algebras and their automorphism groups. London Math. Soc. Monographs 14, Academic Press, London, 1979.Google Scholar
[25] Ringrose, J. R., On the Dixmier approximation theorem. Proc. London Math. Soc. 49(1984), 37–57.Google Scholar