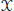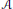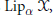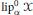Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gordji, Madjid Eshaghi
Jabbari, Ali
and
Kim, Gwang Hui
2015.
SOME CHARACTERIZATIONS OF CHARACTER AMENABLE BANACH ALGEBRAS.
Bulletin of the Korean Mathematical Society,
Vol. 52,
Issue. 3,
p.
761.
Nasr-Isfahani, Rasoul
Nemati, Mehdi
and
Shahmoradi, Somayeh
2016.
Finite dimensional invariant subspaces for algebras of linear operators and amenable Banach algebras.
Linear Algebra and its Applications,
Vol. 510,
Issue. ,
p.
329.
Abtahi, Fatemeh
Azizi,, Mohsen
and
Rejali, Ali
2017.
Character Amenability of the Intersection of Lipschitz Algebras.
Canadian Mathematical Bulletin,
Vol. 60,
Issue. 4,
p.
673.
Abtahi, F.
Byabani, E.
and
Rejali, A.
2019.
Some algebraic and homological properties of Lipschitz algebras and their second duals.
Archivum Mathematicum,
p.
211.
Ebadian, Ali
and
Jabbari, Ali
2022.
Ultrapowers of Banach Algebras.
Vestnik St. Petersburg University, Mathematics,
Vol. 55,
Issue. 3,
p.
336.
Salimi, Solaleh
Mahmoodi, Amin
Sahami, Amir
and
Rostami, Mehdi
2023.
On ϕ-biflatness-like properties of certain Banach algebras with applications.
Filomat,
Vol. 37,
Issue. 11,
p.
3551.
Hamidi Dastjerdi, Fereshteh
and
Soltani Renani, Sima
2025.
Projectivity of some Banach modules over semiprime Banach algebras.
Journal of Algebra and Its Applications,
Vol. 24,
Issue. 02,