Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T15:17:28.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Character Amenability of the Intersection of Lipschitz Algebras

Published online by Cambridge University Press:  20 November 2018

Fatemeh Abtahi ,
Mohsen Azizi  and
Ali Rejali
Fatemeh Abtahi
Affiliation:
Department of Mathematics, University of Isfahan, Isfahan, Iran e-mail: f.abtahi@sci.ui.ac.irm.azizi@sci.ui.ac.irrejali@sci.ui.ac.ir
Mohsen Azizi
Affiliation:
Department of Mathematics, University of Isfahan, Isfahan, Iran e-mail: f.abtahi@sci.ui.ac.irm.azizi@sci.ui.ac.irrejali@sci.ui.ac.ir
Ali Rejali
Affiliation:
Department of Mathematics, University of Isfahan, Isfahan, Iran e-mail: f.abtahi@sci.ui.ac.irm.azizi@sci.ui.ac.irrejali@sci.ui.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 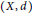$(X,d)$ be a metric space and let 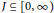$J\subseteq [0,\infty )$ be nonempty. We study the structure of the arbitrary intersections of Lipschitz algebras and define a special Banach subalgebra of 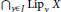${{\cap }_{\gamma \in J\,}}\text{Li}{{\text{p}}_{\gamma \,}}X$, denoted by 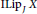$\text{ILi}{{\text{p}}_{J}}X$. Mainly, we investigate the $C$-character amenability of 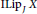$\text{ILi}{{\text{p}}_{J}}X$, in particular Lipschitz algebras. We address a gap in the proof of a recent result in this field. Then we remove this gap and obtain a necessary and sufficient condition for $C$-character amenability of 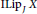$\text{ILi}{{\text{p}}_{J}}X$, specially Lipschitz algebras, under an additional assumption.

Keywords

46H05046J1011J83amenabilitycharacter amenabilityLipschitz algebrametric space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 673 - 689
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Abtahi, F., Amini, H. G., Lotfi, H. A., and Rejali, A., An arbitrary intersection ofLp-spaces. Bull. Aust. Math. Soc. 85(2012), no. 3, 433–445. http://dx.doi.org/10.101 7/S0004972711003510 Google Scholar
[2] Abtahi, F., Amini, H. G., Lotfi, H. A., and Rejali, A., Some intersections of the weighted Lp-spaces. Abstr. Appl. Anal., Article ID 986857, 2013.Google Scholar
[3] Abtahi, F., Amini, H. G., Lotfi, H. A., and Rejali, A., Some intersections ofLorentz spaces. Politehn. Univ. Bucharest Sci. Bull. Ser. A Appl. Math. Phys. 78(2016), no. 3, 73–82. Google Scholar
[4] Bade, W. G., Curtis, P. C. Jr., and Dales, H. G., Amenability and weak amenability for Beurling and Lipschitz algebras. Proc. London Math. Soc. 55(1987), no. 2, 359–377. http://dx.doi.org/10.1093/plms/s3-55_2.359 Google Scholar
[5] Bishop, E. R., Generalized Lipschitz algebras. Canad. Math. Bull. 12(1969), 1–19. http://dx.doi.org/10.41 53/CMB-1 969-001 -2 Google Scholar
[6] Dashti, M., R. Nasr Isfahani, and S. Soltani Renani, Character amenability of Lipschitz algebras. Canad. Math. Bull., 57(2014), no. 1, 37–41. http://dx.doi.org/10.4153/CMB-2O12-01 5-3 Google Scholar
[7] Fukui, K. and T. Nakamura, A topological property of Lipschitz mappings. Topology Appl. 148(2005), 143–152. http://dx.doi.org/10.1016/j.topol.2004.08.005 Google Scholar
[8] E. Gourdeau, , Amenability ofBanach algebras. Math. Proc. Cambridge Philos. Soc. 105(1989), no. 2, 351–355. http://dx.doi.org/10.101 7/S03050041 00067840 Google Scholar
[9] E. Gourdeau, , Amenability ofLipschitz algebras. Math. Proc. Cambridge Philos. Soc. 112(1992), no. 3, 581–588. http://dx.doi.org/10.1017/S0305004100071267 Google Scholar
[10] Hu, Z., Monfared, M. S., and T. Traynor, On character amenable Banach algebras. Studia Math. 193(2009), no. 1, 53–78. http://dx.doi.org/10.4064/sm193-1-3 Google Scholar
[11] Jimenez-Vargas, A. and M. Villegas-Vallecillos, Homomorphisms on real-valued little Lipschitz function spaces. Topology Appl. 156(2009), 2908–2913. http://dx.doi.org/10.101 6/j.topol.2009.01.01 6 Google Scholar
[12] Kaniuth, E., Lau, A. T., and J. Pym, On f-amenability ofBanach algebras. Math. Proc. Cambridge Philos. Soc. 144(2008), no. 1, 85–96. http://dx.doi.org/1 0.101 7/S0305004107000874 Google Scholar
[13] Kaniuth, E., Lau, A. T., and J. Pym, On character amenability ofBanach algebras. J. Math. Anal. Appl. 344(2008), no. 2, 942–955. http://dx.doi.org/10.1016/j.jmaa.2008.03.037 Google Scholar
[14] Miyata, T. and T. Watanabe, Lipschitz functions and approximate resolutions. Topology Appl. 122(2002), 353–375. http://dx.doi.org/1 0.101 6/S01 66-8641 (01 )001 56-0 Google Scholar
[15] Monfared, M. S., Character amenability ofBanach algebras. Math. Proc. Cambridge Philos. Soc. 144(2008), no. 3, 697–706. http://dx.doi.org/10.101 7/S0305004108001126 Google Scholar
[16] Runde, V., Lectures on amenability. Lecture Notes in Mathematics, 1774, Springer-Verlag, Berlin, 2002. http://dx.doi.org/10.1007/b82937 Google Scholar
[17] Sherbert, D. R., Banach algebras of Lipschitz functions. Pacific J. Math. 13(1963), no. 4,1387-1399. http://dx.doi.org/10.2140/pjm.1 963.13.1387 Google Scholar
[18] Sherbert, D. R., The structure of ideals andpoint derivations in Banach algebras of Lipschitz functions. Trans. Amer. Math. Soc. 111(1964), 240–272. http://dx.doi.org/10.1090/S0002-9947-1964-0161177-1 Google Scholar
[19] Zhang, Y., Weak amenability of a class ofBanach algebras. Canad. Math. Bull. 44(2001), no. 4, 504–508. http://dx.doi.org/10.4153/CMB-2001-050-7 Google Scholar