Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T21:18:43.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Character Sums Over Bohr Sets

Published online by Cambridge University Press:  20 November 2018

Brandon Hanson
Brandon Hanson*
Affiliation:
University of Toronto, Toronto, ON M5S 2E4 e-mail: bhanson@math.toronto.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove character sum estimates for additive Bohr subsets modulo a prime. These estimates are analogous to the classical character sum bounds of Pólya–Vinogradov and Burgess. These estimates are applied to obtain results on recurrence 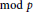$\bmod \,p$ by special elements.

Keywords

11L4011T2411T23character sumsBohr setsfinite fields
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 774 - 786
Copyright
Copyright © Canadian Mathematical Society 2015

References

[B] Bourgain, J., On triples in arithmetic progression. Geom. Funct. Anal. 9(1999), 968–984. http://dx.doi.Org/10.1007/s000390050105 Google Scholar
[BGK] Bourgain, J., Glibichuk, A. A., and Konyagin, S. V., Estimates for the number of sums and products and for exponential sums infields of prime order. J. London Math. Soc. (2) 73(2006), no. 2,380-398. http://dx.doi.Org/10.1112/S0024610706022721 Google Scholar
[BKT] Bourgain, J., Katz, N., and Tao, T., A sum-product estimate in finite fields, and applications. Geom. Funct. Anal. 14(2004), no. 1, 27–57. http://dx.doi.Org/10.1007/s00039-004-0451-1 Google Scholar
[C] Chang, M.-C., On a question of Davenport and Lewis and new character sum bounds infinite fields. Duke Math. J. 145(2008), no. 3, 409–442. http://dx.doi.Org/10.1215/00127094-2008-056 Google Scholar
[CLR] Croot, E., Lyall, N., and Rice, A., A purely combinatorial approach to simultaneous polynomial recurrence modulo 1. arxiv:1307.0779Google Scholar
[G] Garaev, M. Z., An explicit sum-product estimate in Wp. Int. Math. Res. Not. IMRN 2007, no. 11, Art. ID rnmO35.Google Scholar
[GT] Green, B. and Tao, T., New bounds for Szemerédi's theorem. II. A new bound for r4(N). In: Analytic number theory, Cambridge University Press, Cambridge, 2009, pp. 180–204.Google Scholar
[IK] Iwaniec, H. and Kowalski, E., Analytic number theory. American Mathematical Society Colloquium Publications, 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
[KS] Katz, N. H. and C.-Y. Shen, A slight improvement to Garaev's sum product estimate. Proc. Amer. Math. Soc. 136(2008), no. 7, 2499–2504. http://dx.doi.Org/10.1090/S0002-9939-08-09385-4 Google Scholar
[K] Konyagin, S. V., Estimates for character sums in finite fields. (Russian) Mat. Zametki 88(2010), no. 4,529–542; translation in Math. Notes 88(2010), no. 3-4, 503–515. http://dx.doi.Org/10.4213/mzm8852 Google Scholar
[LN] Lidl, R. and Neiderreiter, H., Finite fields. Encyclopedia of Mathematics and its Applications, 20, Cambridge University Press, Cambridge, 1997.Google Scholar
[LM] Lyall, N. and Magyar, A., Simultaneous polynomial recurrence. Bull. Lond. Math. Soc. 43(2011), no. 4, 765–785. http://dx.doi.Org/1 0.1112/blms/bdrO11 Google Scholar
[P] Paley, R. E. A. C., A theorem on characters. J. Lond. Math. Soc. Sl-7(1932), no. 1, 28. http://dx.doi.Org/10.1112/jlms/s1-7.1.28 Google Scholar
[RNRS] Roche-Newton, O., Rudnev, M., and Shkredov, I., New sum-product type estimates over finite fields. arxiv:1408.0542v1Google Scholar
[R] Rudnev, M., An improved sum-product inequality infields of prime order. Int. Math. Res. Not. IMRN 2012, no. 16, 3693–3705.Google Scholar
[Sch] Schmidt, W. M., Small fractional parts of polynomials. Regional Conference Series in Mathematics, 32, American Mathematical Society, 1977.Google Scholar
[Sh] Shao, X., On character sums and exponential sums over generalized arithmetic progressions. Bull. Lond. Math. Soc. 45(2013), no. 3, 541–550. http://dx.doi.Org/10.1112/blms/bds11 5 Google Scholar
[TV] Tao, T. and Vu, V., Additive combinatorics. Cambridge Studies in Advanced Mathematics, 105, Cambridge University Press, Cambridge, 2006. http://dx.doi.Org/!0.1017/CBO9780511755149 Google Scholar