Article contents
A Characterization of Bergman Spaces on the Unit Ball of ℂn . II
Published online by Cambridge University Press: 20 November 2018
Abstract
It has been shown that a holomorphic function 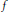 $f$ in the unit ball
$f$ in the unit ball 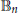 ${{\mathbb{B}}_{n}}$ of
${{\mathbb{B}}_{n}}$ of 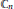 ${{\mathbb{C}}_{n}}$ belongs to the weighted Bergman space
${{\mathbb{C}}_{n}}$ belongs to the weighted Bergman space 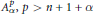 $A_{\alpha }^{p},\,p\,>\,n\,+\,1\,+\alpha $ , if and only if the function
$A_{\alpha }^{p},\,p\,>\,n\,+\,1\,+\alpha $ , if and only if the function 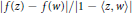 $\left| f(z)\,-\,f(w) \right|/\left| 1\,-\,\left\langle z,\,w \right\rangle\right|$ is in
$\left| f(z)\,-\,f(w) \right|/\left| 1\,-\,\left\langle z,\,w \right\rangle\right|$ is in 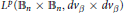 ${{L}^{p}}({{\mathbb{B}}_{n}}\,\times \,{{\mathbb{B}}_{n}},\,d{{v}_{\beta }}\,\times \,d{{v}_{\beta }})$ , where
${{L}^{p}}({{\mathbb{B}}_{n}}\,\times \,{{\mathbb{B}}_{n}},\,d{{v}_{\beta }}\,\times \,d{{v}_{\beta }})$ , where 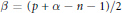 $\beta \,=\,(p\,+\,\alpha \,-\,n\,-\,1)/2$ and
$\beta \,=\,(p\,+\,\alpha \,-\,n\,-\,1)/2$ and 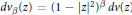 $d{{v}_{\beta }}(z)\,=\,{{(1\,-\,{{\left| z \right|}^{2}})}^{\beta }}\,dv(z)$ . In this paper we consider the range
$d{{v}_{\beta }}(z)\,=\,{{(1\,-\,{{\left| z \right|}^{2}})}^{\beta }}\,dv(z)$ . In this paper we consider the range 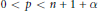 $0\,<\,p\,<\,n\,+\,1\,+\,\alpha $ and show that in this case,
$0\,<\,p\,<\,n\,+\,1\,+\,\alpha $ and show that in this case, 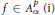 $f\,\in \,A_{\alpha }^{p}\,(\text{i})$ (i) if and only if the function
$f\,\in \,A_{\alpha }^{p}\,(\text{i})$ (i) if and only if the function 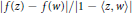 $\left| f(z)\,-\,f(w) \right|/\left| 1\,-\,\left\langle z,\,w \right\rangle\right|$ is in
$\left| f(z)\,-\,f(w) \right|/\left| 1\,-\,\left\langle z,\,w \right\rangle\right|$ is in 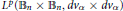 ${{L}^{p}}({{\mathbb{B}}_{n}}\,\times \,{{\mathbb{B}}_{n}},\,d{{v}_{\alpha }}\,\times \,d{{v}_{\alpha }})$ , (ii) if and only if the function
${{L}^{p}}({{\mathbb{B}}_{n}}\,\times \,{{\mathbb{B}}_{n}},\,d{{v}_{\alpha }}\,\times \,d{{v}_{\alpha }})$ , (ii) if and only if the function 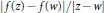 $\left| f(z)\,-\,f(w) \right|/\left| z\,-\,w \right|$ is in
$\left| f(z)\,-\,f(w) \right|/\left| z\,-\,w \right|$ is in 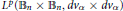 ${{L}^{p}}({{\mathbb{B}}_{n}}\,\times \,{{\mathbb{B}}_{n}},\,d{{v}_{\alpha }}\,\times \,d{{v}_{\alpha }})$ . We think the revealed difference in the weights for the double integrals between the cases
${{L}^{p}}({{\mathbb{B}}_{n}}\,\times \,{{\mathbb{B}}_{n}},\,d{{v}_{\alpha }}\,\times \,d{{v}_{\alpha }})$ . We think the revealed difference in the weights for the double integrals between the cases 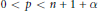 $0\,<\,p\,<\,n\,+\,1\,+\,\alpha $ and
$0\,<\,p\,<\,n\,+\,1\,+\,\alpha $ and 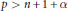 $p\,>\,n\,+\,1\,+\,\alpha $ is particularly interesting.
$p\,>\,n\,+\,1\,+\,\alpha $ is particularly interesting.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
- 8
- Cited by

