Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T05:35:19.484Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of Simple Isolated Line Singularities

Published online by Cambridge University Press:  20 November 2018

Alexandru Zaharia
Alexandru Zaharia*
Affiliation:
Institute of Mathematics, of The Romanian Academy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A line singularity is a function germ 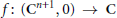$f:\,\left( {{\text{C}}^{n+1}},\,0 \right)\,\to \,\text{C}$ with a smooth 1-dimensional critical set 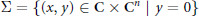$\sum \,=\,\left\{ \left( x,\,y \right)\,\in \,\text{C}\,\times \,{{\text{C}}^{n}}\,|\,y\,=\,0 \right\}$. An isolated line singularity is defined by the condition that for every 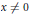$x\,\ne \,0$, the germ of 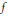$f$ at $\left( x,\,0 \right)$ is equivalent to $y_{1}^{2}\,+\,\cdot \,\cdot \,\cdot \,+\,y_{n}^{2}$. Simple isolated line singularities were classified by Dirk Siersma and are analogous of the famous 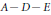$A\,-\,D\,-E$ singularities. We give two new characterizations of simple isolated line singularities.

Keywords

32S2514B05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 4 , 01 December 1999 , pp. 499 - 506
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Arnold, V. I., Normal forms of functions in the neighborhood of critical points. Uspekhi Mat. Nauk (2) 29 (1974), 11–49; RussianMath. Surveys (2) 29 (1974), 18–50.Google Scholar
[2] Arnold, V. I., Gusein-Zade, S. M. and Varchenko, A. N., Singularities of differentiable maps. Vol. 1, Monographs in Math., Birkhauser, 1985.Google Scholar
[3] Durfee, A. H., Fifteen characterizations of rational double points and simple critical points. Enseign. Math. 25 (1979), 131–163.Google Scholar
[4] Goryunov, V. V., Bifurcation diagrams of simple and quasi-homogeneous singularities. Funktsional Anal. i Prilozhen. (2) 17 (1983), 23–37.Google Scholar
[5] Jiang, G., Functions with non-isolated singularities on singular spaces. Thesis, Utrecht University, 1998.Google Scholar
[6] de Jong, T., Some classes of line singularities. Math. Z. 198 (1988), 493–517.Google Scholar
[7] Pellikaan, G. R., Finite determinacy of functions with non-isolated singularities. Proc. London Math. Soc. 57 (1988), 357–382.Google Scholar
[8] Saito, K., Einfach elliptische Singularit¨aten. Invent.Math. 23 (1974), 289–325.Google Scholar
[9] Siersma, D., Isolated line singularities. Proc. of Symposia in Pure Math. (2) 40 (1983), 485–496.Google Scholar
[10] Siersma, D., Quasihomogeneous singularities with transversal type A1. Contemporary Math. 90, (ed. R.Randell), 1989, 261–294.Google Scholar
[11] Stevens, J., Improvements of nonisolated surface singularities. J. London Math. Soc. 39 (1989), 129–144.Google Scholar
[12] Zaharia, A., On simple germs with non-isolated singularities. Math. Scand. 68 (1991), 187–192.Google Scholar