Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schlaepfer, F.
and
Schweppe, F.
1972.
Continuous-time state estimation under disturbances bounded by convex sets.
IEEE Transactions on Automatic Control,
Vol. 17,
Issue. 2,
p.
197.
Fischer, Herbert
1975.
Interval Mathematics.
Vol. 29,
Issue. ,
p.
184.
Fogel, E.
and
Huang, Y.
1980.
Adaptive algorithms for non-stastical parameter estimation in linear models.
Vol. 5,
Issue. ,
p.
1022.
Fogel, Eli
and
Huang, Y.F.
1982.
On the value of information in system identification—Bounded noise case.
Automatica,
Vol. 18,
Issue. 2,
p.
229.
Chernousko, F. L.
1982.
Ellipsoidal bounds for sets of attainability and uncertainty in control problems.
Optimal Control Applications and Methods,
Vol. 3,
Issue. 2,
p.
187.
Fogel, E.
1982.
Membership Set Estimation – An Alternative Approach to System Identification.
IFAC Proceedings Volumes,
Vol. 15,
Issue. 4,
p.
709.
Kai-Bor Yu
1984.
An improved signal restoration method using frequency domain information.
Vol. 9,
Issue. ,
p.
116.
Pierce, Jane E.
and
Rust, Bert W.
1985.
Constrained Least Squares Interval Estimation.
SIAM Journal on Scientific and Statistical Computing,
Vol. 6,
Issue. 3,
p.
670.
Nickel, K. L. E.
1986.
Using Interval Methods for the Numerical Solution of ODE's.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 66,
Issue. 11,
p.
513.
Huang, Y.
1986.
A recursive estimation algorithm using selective updating for spectral analysis and adaptive signal processing.
IEEE Transactions on Acoustics, Speech, and Signal Processing,
Vol. 34,
Issue. 5,
p.
1331.
Pearson, Ronald K.
1988.
Block-Sequential Algorithms for Set-Theoretic Estimation.
SIAM Journal on Matrix Analysis and Applications,
Vol. 9,
Issue. 4,
p.
513.
Deller, J.R.
1989.
Set membership identification in digital signal processing.
IEEE ASSP Magazine,
Vol. 6,
Issue. 4,
p.
4.
Walter, Eric
and
Piet-Lahanier, Hélène
1990.
Estimation of parameter bounds from bounded-error data: a survey.
Mathematics and Computers in Simulation,
Vol. 32,
Issue. 5-6,
p.
449.
Cheung, M.-F.
Yurkovich, S.
and
Passino, K.M.
1991.
An optimal volume ellipsoid algorithm for parameter set estimation.
p.
969.
Preciado, A.
Meizel, D.
Segovia, A.
and
Rombaut, M.
1991.
Fusion of multi-sensor data: a geometric approach.
p.
2806.
Veres, S.M.
and
Norton, J.P.
1991.
Adaptive pole-placement control using parameter bounds.
p.
2860.
Deller, J.R.
Nayeri, M.
and
Odeh, S.F.
1993.
Least-square identification with error bounds for real-time signal processing and control.
Proceedings of the IEEE,
Vol. 81,
Issue. 6,
p.
815.
Cheung, M.-F.
Yurkovich, S.
and
Passino, K.M.
1993.
An optimal volume ellipsoid algorithm for parameter set estimation.
IEEE Transactions on Automatic Control,
Vol. 38,
Issue. 8,
p.
1292.
Neumaier, A.
1993.
Validation Numerics.
Vol. 9,
Issue. ,
p.
175.
Pronzato, Luc
and
Walter, Eric
1994.
Minimal volume ellipsoids.
International Journal of Adaptive Control and Signal Processing,
Vol. 8,
Issue. 1,
p.
15.

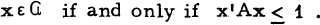
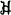 circumscribed about G
circumscribed about G if and only if x'hx ≤ max
if and only if x'hx ≤ max