Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T20:16:11.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Class Number Divisibility in Real Quadratic Function Fields

Published online by Cambridge University Press:  20 November 2018

Christian Friesen
Christian Friesen*
Affiliation:
Mathematics Department University of Toronto Toronto, Ontario Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

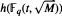Let q be a positive power of an odd prime p, and let Fq(t) be the function field with coefficients in the finite field of q elements. Let denote the ideal class number of the real quadratic function field obtained by adjoining the square root of an even-degree monic 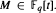. The following theorem is proved: Let n ≧ 1 be an integer not divisible by 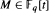p. Then there exist infinitely many monic, squarefree polynomials, such that 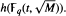n divides the class number, . The proof constructs an element of order n in the ideal class group.

Keywords

11A5511R29Continued FractionsFunction FieldsClass Numbers
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 3 , 01 September 1992 , pp. 361 - 370
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Artin, E., Quadratische Kôrper im Gebiet der hoheren Kongruenzen I, II , Math. Zeitschrift 19(1924) 153–246.Google Scholar
2. Carlitz, L., A class of polynomials , Trans. Amer. Math. Soc. 43(1938) 168–182.Google Scholar
3. Friesen, C., Continued Fractions and Real Quadratic Function Fields Doctoral Thesis, Brown University 1989.Google Scholar
4. Hayes, D. R., Real Quadratic Function Fields , Canadian Mathematical Society Conference Proceedings 7(1985)203–236.Google Scholar
5. Lu, Hong Wen, Divisibility of the Class Number of some real quadratic fields , Acta Math. Sinica 28( 1985) 756–762.Google Scholar
6. Niven, I. and Zuckerman, H. S., An introduction to the Theory of Numbers, edition 4 John Wiley & Sons New York 1980.Google Scholar
7. Perron, O., Die Lehre von den Kettenbriichen Chelsea Publishing New York 1950.Google Scholar