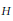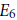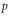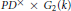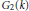Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gan, Wee Teck
2000.
A Siegel-Weil formula for exceptional groups.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2000,
Issue. 528,
Gan, Wee Teck
and
Savin, Gordan
2005.
On minimal representations definitions and properties.
Representation Theory of the American Mathematical Society,
Vol. 9,
Issue. 3,
p.
46.
Gan, Wee Teck
2008.
A Siegel-Weil formula for automorphic characters: Cubic variation of a theme of Snitz.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2008,
Issue. 625,
Gan, Wee Teck
and
Gurevich, Nadya
2009.
Cap representations of G 2 and the spin L-function of PGS p6.
Israel Journal of Mathematics,
Vol. 170,
Issue. 1,
p.
1.
Savin, Gordan
and
Weissman, Martin H.
2011.
Dichotomy for generic supercuspidal representations ofG2.
Compositio Mathematica,
Vol. 147,
Issue. 3,
p.
735.
Pollack, Aaron
2021.
Relative Trace Formulas.
p.
379.
Gan, Wee Teck
and
Savin, Gordan
2023.
Howe duality and dichotomy for exceptional theta correspondences.
Inventiones mathematicae,
Vol. 232,
Issue. 1,
p.
1.