No CrossRef data available.
Article contents
Classification of Inductive Limits of Outer Actions of ℝ on Approximate Circle Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper we present a classification, up to equivariant isomorphism, of 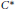 ${{C}^{*}}$-dynamical systems
${{C}^{*}}$-dynamical systems 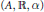 $(A,\,\mathbb{R},\,\alpha )$ arising as inductive limits of directed systems
$(A,\,\mathbb{R},\,\alpha )$ arising as inductive limits of directed systems 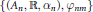 $\{({{A}_{n}},\,\mathbb{R},\,{{\alpha }_{n}}),\,{{\varphi }_{nm}}\}$, where each
$\{({{A}_{n}},\,\mathbb{R},\,{{\alpha }_{n}}),\,{{\varphi }_{nm}}\}$, where each 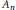 ${{A}_{n}}$ is a finite direct sum of matrix algebras over the continuous functions on the unit circle, and the
${{A}_{n}}$ is a finite direct sum of matrix algebras over the continuous functions on the unit circle, and the 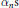 ${{\alpha }_{n}}\text{s}$ are outer actions generated by rotation of the spectrum.
${{\alpha }_{n}}\text{s}$ are outer actions generated by rotation of the spectrum.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
[1] Dean, A. J., Classification of AF flows. Canad. Math. Bull.
46(2003), no. 2, 164–177. doi:10.4153/CMB-2003-018-0Google Scholar
[2] Dean, A. J., Inductive limits of inner actions on approximate interval algebras generated by elements with finite spectrum. J. Ramanujan Math. Soc.
24(2009), no. 4, 323–339.Google Scholar
[3] Dean, A. J., Classification of certain inductive limit type actions of ℝ on C*-algebras. J. Operator Theory
61(2009), no. 2, 439–457.Google Scholar
[4] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew. Math.
443(1993), 179–219. doi:10.1515/crll.1993.443.179Google Scholar
[5] Elliott, G. A., Towards a theory of classification. Adv. Math.
223(2010), no. 1, 30–48. doi:10.1016/j.aim.2009.07.018Google Scholar
[6] Sakai, S., Operator algebras in dynamical systems. The theory of unbounded derivations in C*-algebras. Encyclopedia of Mathematics and its Applications, 41, Cambridge University Press, Cambridge, 1991.Google Scholar


