No CrossRef data available.
Article contents
The Classification of Pin4-Bundles over a 4-Complex
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper we show that the Lie-group 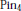 $\text{Pi}{{\text{n}}_{4}}$ is isomorphic to the semidirect product
$\text{Pi}{{\text{n}}_{4}}$ is isomorphic to the semidirect product 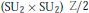 $\text{(S}{{\text{U}}_{2}}\times \text{S}{{\text{U}}_{2}})\text{Z/2}$ where
$\text{(S}{{\text{U}}_{2}}\times \text{S}{{\text{U}}_{2}})\text{Z/2}$ where 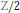 $Z/2$ operates by flipping the factors. Using this structure theorem we prove a classification theorem for
$Z/2$ operates by flipping the factors. Using this structure theorem we prove a classification theorem for 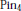 $\text{Pi}{{\text{n}}_{4}}$ -bundles over a finite 4-complex
$\text{Pi}{{\text{n}}_{4}}$ -bundles over a finite 4-complex 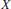 $X$ .
$X$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
[Bro82]
Brown, Kenneth S., Cohomology of Groups. Graduate Texts in Math. 87, Springer-Verlag, New York, Heidelberg, Berlin, 1982.Google Scholar
[DW59]
Dold, A. and Whitney, H., Classification of oriented sphere bundles over a 4-complex. Ann. of Math. (2) 69 (1959), 667–677.Google Scholar
[EM47]
Eilenberg, S. and MacLane, S., Cohomology theory in abstract groups II. Ann. of Math. (2) 48 (1947), 326–41.Google Scholar
[HH58]
Hirzebruch, F. and Hopf, H., Felder von Flächenelementen in 4-dimensionalenMannigfaltigkeiten.Math. Ann. 136 (1958), 156–172.Google Scholar
[LM89]
Blaine Lawson, H. Jr. andMarie-LouiseMichelson, Spin Geometry. Princeton Math. Ser. 38, Princeton Univ. Press, Princeton, New Jersey, 1989.Google Scholar
[Web96]
Weber, Christian, Gauge theory on nonorientable four-manifolds. Verlag (ed. Dr. Kovăc), Hamburg, 1996.Google Scholar

