Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T08:59:26.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Cockcroft Properties of Thompson’s Group

Published online by Cambridge University Press:  20 November 2018

W. A. Bogley ,
N. D. Gilbert  and
James Howie
W. A. Bogley
Affiliation:
Department of Mathematics, Kidder 368, Oregon State University, Corvallis, OR 97331-4605, USA, email: bogley@math.orst.edu
N. D. Gilbert
Affiliation:
Department of Mathematics, Heriot-Watt University, Riccarton, Edinburgh EH14 4AS, Scotland, email: N.D.Gilbert@hw.ac.uk
James Howie
Affiliation:
Department of Mathematics, Heriot-Watt University, Riccarton, Edinburgh EH14 4AS, Scotland, email: J.Howie@hw.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a study of the word problem for groups, R. J. Thompson considered a certain group 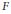$F$ of self-homeomorphisms of the Cantor set and showed, among other things, that 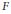$F$ is finitely presented. Using results of K. S. Brown and R. Geoghegan, M. N. Dyer showed that 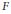$F$ is the fundamental group of a finite two-complex 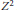${{Z}^{2}}$ having Euler characteristic one and which is Cockcroft, in the sense that each map of the two-sphere into 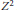${{Z}^{2}}$ is homologically trivial. We show that no proper covering complex of 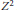${{Z}^{2}}$ is Cockcroft. A general result on Cockcroft properties implies that no proper regular covering complex of any finite two-complex with fundamental group 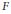$F$ is Cockcroft.

Keywords

57M2020F3857M1020F34two-complexcovering spaceCockcroft two-complexThompson’s group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 3 , 01 September 2000 , pp. 268 - 281
Copyright
Copyright © Canadian Mathematical Society 2000

References

[Bri] Brin, M. G., The ubiquity of Thompson's group F in groups of piecewise linear homeomorphisms of the unit interval. MAGNUS preprint 97-05-04A.Google Scholar
[Bro] Brown, K. S., Finiteness properties of groups. J. Pure Appl. Algebra 44 (1987), 45–75.Google Scholar
[BG] Brown, K. S. and R. Geoghegan, An infinite-dimensional torsion-free FP∞ group. Invent.Math. 77 (1984), 367–381.Google Scholar
[DGH] Duncan, A. J., Gilbert, N. D., and Howie, J., Problem Session. In: Combinatorial and Geometric Group Theory, Edinburgh 1993; LondonMath. Soc. Lecture Note Ser. 204(1995), Cambridge University Press, 322–325.Google Scholar
[D] Dyer, M. N., Cockcroft 2-complexes. Preprint (University of Oregon, 1993).Google Scholar
[GH] Gilbert, N. D. and Howie, J., Threshold subgroups for Cockcroft 2-complexes. Comm. Algebra 22 (1995), 255–275.Google Scholar
[H] Harlander, J.,Minimal Cockcroft subgroups. Glasgow Math. J. 36 (1994), 87–90.Google Scholar
[K] Kaplansky, I., Fields and Rings. University of Chicago Press, 1972.Google Scholar
[M] Montgomery, M. S., Left and right inverses in group algebras. Bull. Amer. Math. Soc. 75 (1969), 539–540.Google Scholar
[P] Pride, S. J., Examples of presentations that are minimally Cockcroft in several different ways. J. Pure and Appl. Algebra 88 (1993), 199–204.Google Scholar
[T] Thompson, R. J., Embeddings into finitely presented simple groups which preserve the word problem. In: Word Problems II (eds. S. I. Adian, W.W. Boone, and G. Higman), North-Holland, 1980, 401–441.Google Scholar
[W] Whitehead, J. H. C., On adding relations to homotopy groups. Ann. of Math. 42 (1941), 409–428.Google Scholar