Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T00:56:54.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomogeneity One Randers Metrics

Published online by Cambridge University Press:  20 November 2018

Jifu Li ,
Zhiguang Hu  and
Shaoqiang Deng
Jifu Li
Affiliation:
School of Mathematical Sciences and LPMC, Nankai University, Tianjin 300071, People's Republic of China and School of Science, Tianjin University of Technology, Tianjin 30084, People's Republic of China e-mail: lijifu@mail.nankai.edu.cn
Zhiguang Hu
Affiliation:
College of Mathematics, Tianjin Normal University, Tianjin 300387, P.R. China e-mail: nankaitaiji@mail.nankai.edu.cn
Shaoqiang Deng
Affiliation:
School of Mathematical Sciences and LPMC, Nankai University, Tianjin 300071, People's Republic of China e-mail: dengsq@nankai.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An action of a Lie group $G$ on a smooth manifold 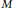$M$ is called cohomogeneity one if the orbit space 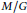${M}/{G}\;$ is of dimension 1. A Finsler metric 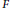$F$ on 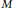$M$ is called invariant if 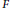$F$ is invariant under the action of $G$. In this paper, we study invariant Randers metrics on cohomogeneity one manifolds. We first give a sufficient and necessary condition for the existence of invariant Randers metrics on cohomogeneity one manifolds. Then we obtain some results on invariant Killing vector fields on the cohomogeneity one manifolds and use them to deduce some sufficient and necessary conditions for a cohomogeneity one Randers metric to be Einstein.

Keywords

53C3053C60Cohomogeneity one actionsnormal geodesicsinvariant vector fieldsRanders metrics
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 575 - 584
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Akbar-Zadeh, H., Sur les espaces de Finslerà courbures sectionnelles constantes. Acad. Roy. Belg. Bull. Cl. Sci. 74(1988), no. 10, 281–322.Google Scholar
[2] Alekseevsky, A. V. and Alekseevsky, D. V., G-manifolds with one dimensional orbit space. In: Lie groups, their discrete subgroups, and invariant theory, Adv. Soviet Math., 8, American Mathematical Society, Providence, RI, 1992, pp. 1–31.Google Scholar
[3] Alekseevsky, A. V. and Alekseevsky, D. V., Riemannian G-manifold with one-dimensional orbit space. Ann. Glob. Anal.Geom. 11(1993), no. 3,197-211.Google Scholar
[4] Alekseevsky, D. V., Riemannian manifolds of cohomogeneity one. In: Differential geometry and its applications (Eger, 1989), Colloq. Math. Soc. JânosBolyai, 56, North-Holland, Amsterdam, 1992, pp. 9–22.Google Scholar
[5] Bao, D. and Robles, C., Ricci and flag curvatures in Finsler geometry. In: A sampler of Riemann-Finsler geometry, Math. Sci. Res. Inst. Publ., 50, Cambridge University Press, Cambridge, 2004, pp. 197–260.Google Scholar
[6] Bao, D., Robles, C., and Shen, Z., Zermelo navigation on Riemannian manifolds. J. Differential Geom. 66(2004), 377–435.Google Scholar
[7] Bèrard Bergery, L., Sur les nouvelles variétés riemanniennes d'Einstein. Publ. Inst. E. Cartan. 4(1982), 1–60.Google Scholar
[8] Bishop, R. L. and B. O'Neill, Manifolds of negative curvature. Trans. Amer. Math. Soc. 145(1969), 1–49. http://dx.doi.org/10.1090/S0002-9947-1969-0251664-4 Google Scholar
[9] Deng, S., Homogeneous Finsler spaces. Springer Monographs in Mathematics, Springer, New York, 2012.Google Scholar
[10] Deng, S. and Hou, Z., Invariant Randers metrics on homogeneous Riemanniann manifold. J. Phys. A 37(2004), no. 15, 4353–4360; Corrigendum, J. Phys.A 39(2006), no. 18, 5249-5250. http://dx.doi.org/10.1088/0305-4470/37/1 5/004 Google Scholar
[11] Deng, S. and Hou, Z., Homogeneous Einstein-Randers spaces of negative Ricci curvature. C. R. Math. Acad. Sci. Paris. 347(2009), 1169–1172. http://dx.doi.org/10.101 6/j.crma.2009.08.006 Google Scholar
[12] Galaz-Garcia, E. and Searle, C., Cohomogeneity one Alexandrov spaces. Transform. Groups 16(2011), no. 1, 91–107. http://dx.doi.org/10.1007/s00031-011-9122-0 Google Scholar
[13] Grove, K., Verdiani, L., Wilking, B., and Ziller, W., Non-negative curvature obstruction in cohomogeneity one and the Kervaire spheres. Ann. Sc. Norm. Super. Pisa Cl. Sci. 5(2006), no. 2, 159–170.Google Scholar
[14] Grove, K., Wilking, B., and Ziller, W., Positively curved cohomogeneity one manifolds and 3-Sasakian geometry.J. Differential Geom. 78(2008), no. 1, 33–111.Google Scholar
[15] Grove, K. and Ziller, W., Curvature and symmetry ofMilnor spheres. Ann. of Math. 152(2000), no. 1, 331–367. http://dx.doi.org/10.2307/2661385 Google Scholar
[16] Grove, K. and Ziller, W., Cohomogeneity one manifolds with positive Ricci curvature. Invent. Math. 149(2002), no. 3, 619–646. http://dx.doi.org/10.1007/s002220200225 Google Scholar
[17] Hsiang, W. Y. and Lawson, B., Minimal submanifolds in low cohomogeneity. J. Differential Geometry 5(1971), 1–38.Google Scholar
[18] Kobayashi, S., Transformation groups in differential geometry. Classics in Mathematics. Springer-Verlag, Berlin, 1995.Google Scholar
[19] Mostert, P. S., On a compact Lie group acting on a manifold. Ann. of Math. 65(1957), 447–455. http://dx.doi.org/10.2307/1 970056 Google Scholar
[20] O'Neill, B., Semi-Riemannian geometry. With applications to relativity.Pure and Applied Mathematics, 103, Academic Press, New York, 1983.Google Scholar
[21] Podesta, E. and Verdiani, L., Positively curved 1'-dimensional manifolds. Quart. J. Math. Oxford. Ser. 50(1999), no. 200, 497–504. http://dx.doi.org/10.1093/qjmath/50.200.497 Google Scholar
[22] Sanchez, M., On the geometry of generalized Robertson-Walker spacetimes: curvature and Killing fields. J. Geom. Phys. 31(1999), no. 1, 1–15. http://dx.doi.org/10.101 6/S0393-0440(98)00061 -8 Google Scholar
[23] Searle, C., Cohomogeneity one and positive curvature in low dimension. Math. Z. 214(1993), no. 3, 491–498; Corrigendum, 226(1997), no. 1,165-167.Google Scholar
[24] Verdiani, L., Cohomogeneity one Riemannian manifolds of even dimension with strictly positive sectional curvature. I. Math. Z. 241(2002), no. 2, 329–339. http://dx.doi.org/10.1007/s00209020041 7 Google Scholar
[25] Verdiani, L., Cohomogeneity one manifolds of even dimension strictly positive sectional curvature. J. Differential Geom. 68(2004), no. 1, 31–72.Google Scholar
[26] Wang, H., Huang, L., and Deng, S., Homogeneous Einstein-Randers metrics on spheres. Nonlinear Anal.74(2011), no. 17, 6295–6301.http://dx.doi.org/10.1016/j.na.2011.06.008 Google Scholar
[27] Ziller, W., On the geometry of cohomogeneity one manifolds with positive curvature. In: Riemannian topology and geometric structures on manifolds.Progr. Math., 271, Birkhaser Boston, Boston, MA, 2009, pp. 233–262.Google Scholar