Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T13:44:04.204Z Has data issue: false hasContentIssue false
  • English
  • Français

Cokernels of Homomorphisms from Burnside Rings to Inverse Limits

Published online by Cambridge University Press:  20 November 2018

Masaharu Morimoto
Masaharu Morimoto*
Affiliation:
Graduate School of Natural Science and Technology, Okayama University, Tsushimanaka 3-1-1, Kitaku, Okayama, 700-8530Japan e-mail: morimoto@ems.okayama-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 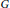$G$ be a finite group and let 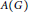$A\left( G \right)$ denote the Burnside ring of 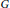$G$. Then an inverse limit 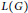$L\left( G \right)$ of the groups 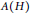$A\left( H \right)$ for proper subgroups 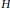$H$ of 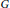$G$ and a homomorphism res from 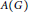$A\left( G \right)$ to 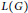$L\left( G \right)$ are obtained in a natural way. Let 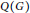$Q\left( G \right)$ denote the cokernel of res. For a prime 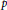$p$, let 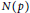$N\left( p \right)$ be the minimal normal subgroup of 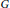$G$ such that the order of 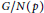${G}/{N}\;\left( p \right)$ is a power of 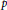$p$, possibly 1. In this paper we prove that 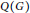$Q\left( G \right)$ is isomorphic to the cartesian product of the groups 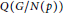$Q\left( {G}/{N\left( p \right)}\; \right)$, where 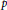$p$ ranges over the primes dividing the order of 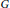$G$.

Keywords

19A2257S17Burnside ringinverse limitfinite group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 165 - 172
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bak, A., K-theory of forms. Annals of Mathematics Studies, 98, Princeton University Press, Princeton, NJ, 1981.Google Scholar
[2] Bak, A., Induction for finite groups revisited. J. Pure Appl. Algebra 104(1995), 235–241. http://dx.doi.Org/1 0.101 6/0022-4049(94)00137-5 Google Scholar
[3] torn Dieck, T., Transformation groups. De Gruyter Studies in Mathematics, 8, Walter de Gruyter, Berlin, 1987. http://dx.doi.Org/10.1515/9783110858372.312 Google Scholar
[4] Dress, A., A characterization of solvable groups. Math. Z. 110(1969), 213–217. http://dx.doi.Org/1 0.1007/BF01110213 Google Scholar
[5] Hara, Y. and Morimoto, M., The inverse limit of the Burnside ring for a family of subgroups ofG. Hokkaido Math. J., to appear.Google Scholar
[6] Kratzer, C. and J. Thévenaz, Fonction de Môbius d'un groupe fini et anneau de Burnside. Comment. Math. Helv. 59(1984), 425–438. http://dx.doi.Org/10.1 007/BF02566359 Google Scholar
[7] Laitinen, E. and Morimoto, M., Finite groups with smooth one fixed point actions on spheres. Forum Math. 10(1998), 479–520. http://dx.doi.Org/10.1515/form.10.4.479 Google Scholar
[8] Morimoto, M., The Burnside ring revisited. In: Current trends in transformation groups, Jf-Monogr. Math., 7, Kluwer Academic Publ., Dordrecht-Boston, 2002, pp. 129–145. http://dx.doi.Org/10.1007/978-94-009-0003-5_9 Google Scholar
[9] Morimoto, M., Direct limits and inverse limits of Mackey functors. J. Algebra 470(2017), 68–76. http://dx.doi.Org/1 0.101 6/j.jalgebra.2O1 6.09.002 Google Scholar
[10] Oliver, R., Fixed point sets of groups on finite acyclic complexes. Comment. Math. Helv. 50(1975), 155–177. http://dx.doi.Org/10.1007/BF02565743 Google Scholar