Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T06:05:02.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Commutators and Analytic Dependence of Fourier-Bessel Series on (0, ∞)

Published online by Cambridge University Press:  20 November 2018

José J. Guadalupe ,
Mario Pérez  and
Juan L. Varona
José J. Guadalupe
Affiliation:
Dpto. de Matemáticas y Computaciòn Universidad de La Rioja 26004 Logroño Spain
Mario Pérez
Affiliation:
Dpto. de Matemáticas Universidad de Zaragoza 50009 Zaragoza Spain, email: mperez@posta.unizar.es
Juan L. Varona
Affiliation:
Dpto. de Matemáticas y Computaciòn Universidad de La Rioja 26004 Logroño Spain, email: jvarona@dmc.unirioja.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the boundedness of the commutators 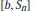$[b,\,{{S}_{n}}]$ where $b$ is a 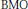$\text{BMO}$ function and 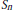${{S}_{n}}$ denotes the 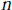$n$-th partial sum of the Fourier-Bessel series on 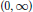$(0,\,\infty )$. Perturbing the measure by 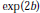$\text{exp(}2\text{b)}$ we obtain that certain operators related to 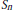${{S}_{n}}$ depend analytically on the functional parameter $b$.

Keywords

42C10Fourier-Bessel seriescommutatorsBMOAp weights
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 198 - 208
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Aptekarev, A. I., Branquinho, A. and Marcellán, F., Toda-type differential equations for the recurrence coefficients of orthogonal polynomials and Freud transformation. J. Comput. Appl. Math. 78 (1997), 139–160.Google Scholar
[2] Bloom, S., A commutator theorem and weighted BMO. Trans. Amer. Math. Soc. 292 (1985), 103–122.Google Scholar
[3] Coifman, R. R. and Murray, M. A. M., Uniform analyticity of orthogonal projections. Trans. Amer.Math. Soc. 312 (1989), 779–817.Google Scholar
[4] Coifman, R. R., Rochberg, R. and Weiss, G., Factorization theorems for Hardy spaces in several variables. Ann. of Math. 103 (1976), 611–635.Google Scholar
[5] Còrdoba, A., The disc multiplier. Duke Math. J. 58 (1989), 21–29.Google Scholar
[6] Garcìa-Cuerva, J. and de Francia, J. L. Rubio, Weighted norm inequalities and related topics. North-Holland, Amsterdam, 1985.Google Scholar
[7] Marcellán, F., Dehesa, J. S. and Ronveaux, A., On orthogonal polynomials with perturbed recurrence relations. J. Comput. Appl. Math. 30 (1990), 203–212.Google Scholar
[8] Neugebauer, C. J., Inserting Ap weights. Proc. Amer. Math. Soc. 87 (1983), 644–648.Google Scholar
[9] Nevai, P. and Van Assche, W., Compact perturbations of orthogonal polynomials. Pacific J. Math. 153 (1992), 163–184.Google Scholar
[10] Segovia, C. and Torrea, J. L., Vector-valued commutators and applications. Indiana Univ. Math. J. 38 (1989), 959–971.Google Scholar
[11] Segovia, C. and Torrea, J. L., Weighted inequalities for commutators of fractional and singular integrals. Publ.Mat. 35 (1991), 209–235.Google Scholar
[12] Segovia, C. and Torrea, J. L., Higher order commutators for vector-valued Calderòn-Zygmund operators. Trans. Amer.Math. Soc. 336 (1993), 537–556.Google Scholar
[13] Varona, J. L., Fourier series of functions whose Hankel transform is supported on [0, 1]. Constr. Approx. 10 (1994), 65–75.Google Scholar
[14] Watson, G. N., A treatise on the theory of Bessel functions. 2nd edn, Cambridge University Press, Cambridge, 1944 (reprinted 1995).Google Scholar