No CrossRef data available.
Article contents
Composition operators on weighted analytic spaces
Published online by Cambridge University Press: 17 April 2023
Abstract
We characterize the membership in the Schatten ideals 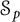 $\mathcal {S}_p$,
$\mathcal {S}_p$, 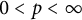 $0<p<\infty $, of composition operators acting on weighted Dirichlet spaces. Our results concern a large class of weights. In particular, we examine the case of perturbed superharmonic weights. Characterization of composition operators acting on weighted Bergman spaces to be in
$0<p<\infty $, of composition operators acting on weighted Dirichlet spaces. Our results concern a large class of weights. In particular, we examine the case of perturbed superharmonic weights. Characterization of composition operators acting on weighted Bergman spaces to be in 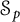 $\mathcal {S}_p$ is also given.
$\mathcal {S}_p$ is also given.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Aleman, A.,
Hilbert spaces of analytic functions between the Hardy and the Dirichlet space
. Proc. Amer. Math. Soc. 115(1992), 97–104.CrossRefGoogle Scholar
Aleman, A., The multiplication operator on Hilbert spaces of analytic functions, Habilitationsschrift, Fern Universitat, Hagen, 1993.Google Scholar
Aleman, A. and Constantin, O.,
Spectra of integration operators on weighted Bergman spaces
. J. Anal. Math. 109(2009), 199–231.CrossRefGoogle Scholar
Aleman, A., Pott, S., and Reguera, M. C.,
Characterizations of a limiting class B
 ${}_{\infty }$
of Békollé–Bonami weights
. Rev. Mat. Iberoam. 35(2019), 1766–1692.CrossRefGoogle Scholar
${}_{\infty }$
of Békollé–Bonami weights
. Rev. Mat. Iberoam. 35(2019), 1766–1692.CrossRefGoogle Scholar
Bao, G., Göğüş, N. G., and Pouliasis, S.,
On Dirichlet spaces with a class of superharmonic weights
. Canad. J. Math. 70(2018), 721–741.CrossRefGoogle Scholar
Bao, G., Wulan, H., and Zhu, K.,
A Hardy–Littlewood theorem for Bergman spaces
. Ann. Acad. Sci. Fenn. Math. 43(2018), 807–821.CrossRefGoogle Scholar
Bourass, M. and Marrhich, I., Littlewood–Paley estimates with applications to Toeplitz and integration operators on weighted Bergman spaces. Banach J. Math. Anal. 17(2023), 10.CrossRefGoogle Scholar
Constantin, O.,
Carleson embeddings and some classes of operators on weighted Bergman spaces
. J. Math. Anal. Appl. 365(2010), 668–682.CrossRefGoogle Scholar
Cowen, C. C. and MacCluer, B., Composition operators on spaces of analytic functions, Studies in Advanced Mathematics, CRC Press, Boca Raton, 1995.Google Scholar
El-Fallah, O. and ElIbbaoui, M.,
Trace estimates of Toeplitz operators on Bergman spaces and applications to composition operators
. Rev. Mat. Iberoam. 38(2022), 1723–1762.CrossRefGoogle Scholar
El-Fallah, O., Mahzouli, H., Marrhich, I., and Naqos, H.,
Asymptotic behavior of eigenvalues of Toeplitz operators on the weighted analytic spaces
. J. Funct. Anal. 270(2016), 4614–4630.CrossRefGoogle Scholar
El-Fallah, O., Mahzouli, H., Marrhich, I., and Naqos, H.,
Toeplitz operators on harmonically weighted Bergman spaces and applications to composition operators on Dirichlet spaces
. J. Math. Anal. Appl. 466(2018), 471–489.CrossRefGoogle Scholar
Esmaeili, K. and Kellay, K.,
Weighted composition operators on weighted Bergman and Dirichlet spaces
. Canad. Math. Bull. 66(2023), 286–302.CrossRefGoogle Scholar
Fàbrega, J. and Ortega, J. M.,
Pointwise multipliers and corona type decomposition in BMOA
. Ann. Inst. Fourier (Grenoble) 46(1996), 111–137.Google Scholar
Kellay, K. and Lefèvre, P.,
Compact composition operators on weighted Hilbert spaces of analytic functions
. J. Math. Anal. Appl. 386(2012), 718–727.CrossRefGoogle Scholar
Lefèvre, P., Li, D., Queffélec, H., and Rodríguez-Piazza, L.,
Approximation numbers of composition operators on the Dirichlet space
. Ark. Mat. 53(2015), 155–175.CrossRefGoogle Scholar
Liu, X., Chacón, G., and Lou, Z.,
Characterizations of the Dirichlet-type space
. Complex Anal. Oper. Theory 9(2015), 1269–1286.CrossRefGoogle Scholar
Luecking, D. H.,
Representation and duality in weighted spaces of analytic functions
. Indiana Univ. Math. J. 34(1985), 319–336.CrossRefGoogle Scholar
Luecking, D. H. and Zhu, K.,
Composition operators belonging to the Schatten ideals
. Amer. J. Math. 114(1992), 1127–1145.CrossRefGoogle Scholar
Oleinik, V. L.,
Embedding theorems for weighted classes of harmonic and analytic functions
. J. Soviet Math. 9(1978), 228–243.CrossRefGoogle Scholar
Pau, J. and Pérez, P. A.,
Composition operators acting on weighted Dirichlet spaces
. J. Math. Anal. Appl. 401(2013), 682–694.CrossRefGoogle Scholar
Peláez, J. A.,
Small weighted Bergman spaces
. In: Proceedings of the summer school in complex and harmonic analysis, and related topics, University of Eastern Finland, Joensuu (2016), 29–98.Google Scholar
Peláez, J. A. and Rättyä, J.,
Trace class criteria for Toeplitz and composition operators on small Bergman spaces
. Adv. Math. 293(2016), 606–643.CrossRefGoogle Scholar
Sarason, D. and Silva, O.,
Composition operators on a local Dirichlet space
. J. Anal. Math. 87(2002), 433–450.CrossRefGoogle Scholar
Shapiro, J. H.,
The essential norm of a composition operator
. Ann. Math. 125(1987), 375–404.CrossRefGoogle Scholar
Shapiro, J. H., Composition operators and classical function theory, Springer, New York, 1993.CrossRefGoogle Scholar
Zorboska, N.,
Composition operators on weighted Dirichlet spaces
. Proc. Amer. Math. Soc. 126(1998), 2013–2023.CrossRefGoogle Scholar



