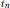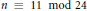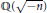Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Konstantinou, Elisavet
and
Kontogeorgis, Aristides
2010.
Ramanujan’s class invariants and their use in elliptic curve cryptography.
Computers & Mathematics with Applications,
Vol. 59,
Issue. 8,
p.
2901.
Konstantinou, Elisavet
and
Kontogeorgis, Aristides
2011.
Some remarks on the construction of class polynomials.
Advances in Mathematics of Communications,
Vol. 5,
Issue. 1,
p.
109.
Chan, Heng Huat
Konstantinou, Elisavet
Kontogeorgis, Aristides
and
Tan, Chik How
2012.
What is your “birthday elliptic curve”?.
Finite Fields and Their Applications,
Vol. 18,
Issue. 6,
p.
1232.
KONSTANTINOU, ELISAVET
and
KONTOGEORGIS, ARISTIDES
2012.
RAMANUJAN INVARIANTS FOR DISCRIMINANTS CONGRUENT TO 5 (mod 24).
International Journal of Number Theory,
Vol. 08,
Issue. 01,
p.
265.
Kontogeorgis, Aristides
2013.
Constructing class invariants.
Mathematics of Computation,
Vol. 83,
Issue. 287,
p.
1477.
Hu, Jian Jun
2014.
Constructing Elliptic Curves over Ramanujan's Class Invariants.
Advanced Materials Research,
Vol. 915-916,
Issue. ,
p.
1336.
Konstantinou, Elisavet
and
Kontogeorgis, Aristides
2015.
Computation, Cryptography, and Network Security.
p.
299.
Laurens, Thierry
2022.
KdV on an incoming tide.
Nonlinearity,
Vol. 35,
Issue. 1,
p.
343.
CHAVAN, SARTH
2023.
ON DISCRIMINANTS OF MINIMAL POLYNOMIALS OF THE RAMANUJAN CLASS INVARIANTS.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 2,
p.
264.