Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-12T22:42:28.958Z Has data issue: false hasContentIssue false
  • English
  • Français

A conjecture strengthening the Zariski dense orbit problem for birational maps of dynamical degree one

Part of: Arithmetic algebraic geometry Abelian varieties and schemes Rings and algebras arising under various constructions Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  07 July 2022

Jason Bell Open the ORCID record for Jason Bell [Opens in a new window]  and
Dragos Ghioca
Jason Bell
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON N2L 3G1, Canada e-mail: jpbell@uwaterloo.ca
Dragos Ghioca*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, Canada
*
e-mail: dghioca@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We formulate a strengthening of the Zariski dense orbit conjecture for birational maps of dynamical degree one. 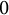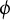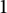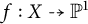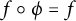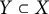So, given a quasiprojective variety X defined over an algebraically closed field K of characteristic $0$ , endowed with a birational self-map $\phi $ of dynamical degree $1$ , we expect that either there exists a nonconstant rational function $f:X\dashrightarrow \mathbb {P} ^1$ such that $f\circ \phi =f$ , or there exists a proper subvariety $Y\subset X$ with the property that, for any invariant proper subvariety 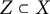$Z\subset X$ , we have that $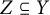Z\subseteq Y$ . We prove our conjecture for automorphisms 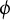$\phi $ of dynamical degree 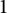$1$ of semiabelian varieties X. Moreover, we prove a related result for regular dominant self-maps 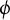$\phi $ of semiabelian varieties X: assuming that 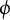$\phi $ does not preserve a nonconstant rational function, we have that the dynamical degree of 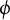$\phi $ is larger than 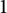$1$ if and only if the union of all 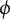$\phi $ -invariant proper subvarieties of X is Zariski dense. We give applications of our results to representation-theoretic questions about twisted homogeneous coordinate rings associated with abelian varieties.

Keywords

Semiabelian varietiesendomorphismsdynamical degreedense orbitsDixmier–Moeglin equivalence

MSC classification

Primary: 11G10: Abelian varieties of dimension $> 1$ 14K12: Subvarieties 37P55: Arithmetic dynamics on general algebraic varieties
Secondary: 16S38: Rings arising from non-commutative algebraic geometry
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 477 - 491
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors were partially supported by Discovery Grants from the National Science and Engineering Research Council of Canada.

References

Amerik, E. and Campana, F., Fibrations méromorphes Sur certaines variétés à fibré canonique trivial . Pure Appl. Math. Q. 4(2008), no. 2, 509–545, Special Issue: In honor of Fedor Bogomolov. Part 1.CrossRefGoogle Scholar
Artin, M., Tate, J., and Van den Bergh, M., Some algebras associated to automorphisms of elliptic curves . In: The Grothendieck Festschrift, Vol. I, Birkhäuser Boston, Boston, MA, 1990, pp. 33–85.Google Scholar
Artin, M. and Van den Bergh, M., Twisted homogeneous coordinate rings. J. Algebra 133(1990), 249–271.CrossRefGoogle Scholar
Bell, J. and Ghioca, D., Periodic subvarieties of semiabelian varieties and annihilators of irreducible representations . Adv. Math. 349(2019), 459–487.CrossRefGoogle Scholar
Bell, J., Launois, S., León Sánchez, O., and Moosa, R., Poisson algebras via model theory and differential-algebraic geometry . J. Eur. Math. Soc. (JEMS) 19(2017), 2019–2049.10.4171/JEMS/712CrossRefGoogle Scholar
Bell, J. P., Ghioca, D., and Reichstein, Z., On a dynamical version of a theorem of Rosenlicht . Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 17(2017), no. 1, 187–204.Google Scholar
Bell, J. P., Ghioca, D., Reichstein, Z., and Satriano, M., On the Medvedev–Scanlon conjecture for minimal threefolds of non-negative Kodaira dimension . New York J. Math. 23(2017), 1185–1203.Google Scholar
Bell, J. P., Rogalski, D., and Sierra, S. J., The Dixmier–Moeglin equivalence for twisted homogeneous coordinate rings . Israel J. Math. 180(2010), 461–507.CrossRefGoogle Scholar
Brown, K. A. and Goodearl, K. R., Lectures on algebraic quantum groups, Advanced Courses in Mathematics, CRM Barcelona, Birkhäuser Verlag, Basel, 2002.CrossRefGoogle Scholar
Cantat, S., Invariant hypersurfaces in holomorphic dynamics . Math. Res. Lett. 17(2010), no. 5, 833–841.CrossRefGoogle Scholar
Corvaja, P., Ghioca, D., Scanlon, T., and Zannier, U., The dynamical Mordell–Lang conjecture for endomorphisms of semiabelian varieties defined over fields of positive characteristic . J. Inst. Math. Jussieu 20(2021), no. 2, 669–698.10.1017/S1474748019000318CrossRefGoogle Scholar
Dang, N.-B., Ghioca, D., Hu, F., Lesieutre, J., and Satriano, M., Higher arithmetic degrees of dominant rational self-maps . Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 23(2022), 465–483.Google Scholar
Diller, J. and Favre, C., Dynamics of bimeromorphic maps of surfaces . Amer. J. Math. 123(2001), 1135–1169.10.1353/ajm.2001.0038CrossRefGoogle Scholar
Dixmier, J., Idéaux primitifs dans les algèbres enveloppantes . J. Algebra 48(1977), 96–112.CrossRefGoogle Scholar
Ghioca, D. and Hu, F., Density of orbits of endomorphisms of commutative linear algebraic groups . New York J. Math. 24(2018), 375–388.Google Scholar
Ghioca, D. and Saleh, S., Zariski dense orbits for regular self-maps of tori in positive characteristic . New York J. Math. 27(2021), 1274–1304.Google Scholar
Ghioca, D. and Saleh, S., Zariski dense orbits for regular self-maps on split semiabelian varieties . Canad. Math. Bull. 65(2022), no. 1, 116–122.CrossRefGoogle Scholar
Ghioca, D. and Satriano, M., Density of orbits of dominant regular self-maps of semiabelian varieties . Trans. Amer. Math. Soc. 371(2019), no. 9, 6341–6358.CrossRefGoogle Scholar
Ghioca, D. and Scanlon, T., Density of orbits of endomorphisms of abelian varieties . Trans. Amer. Math. Soc. 369(2017), no. 1, 447–466.CrossRefGoogle Scholar
Ghioca, D. and Xie, J., Algebraic dynamics of skew-linear self-maps . Proc. Amer. Math. Soc. 146(2018), no. 10, 4369–4387.CrossRefGoogle Scholar
Goodearl, K. R. and Letzter, E. S., The Dixmier–Moeglin equivalence in quantum coordinate rings and quantized Weyl algebras , Trans. Amer. Math. Soc. 352(2000), 1381–1403.10.1090/S0002-9947-99-02345-4CrossRefGoogle Scholar
Harris, J., Algebraic geometry. A first course, Graduate Texts in Mathematics, 133, Springer-Verlag, New York, 1995.Google Scholar
Iitaka, S., Logarithmic forms of algebraic varieties . J. Fac. Sci. Univ. Tokyo Sect. IA Math. 23(1976), 525–544.Google Scholar
Keeler, D. S., Criteria for $\sigma$ -ampleness . J. Amer. Math. Soc. 13(2000), 517–532.CrossRefGoogle Scholar
Matsuzawa, Y. and Sano, K., Arithmetic and dynamical degrees of self-morphisms of semi-abelian varieties . Ergodic Theory Dynam. Systems 40(2020), no. 6, 1655–1672.CrossRefGoogle Scholar
McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings, American Mathematical Society, Providence, RI, 2001.CrossRefGoogle Scholar
Medvedev, A. and Scanlon, T., Invariant varieties for polynomial dynamical systems . Ann. Math. 179(2014), no. 1, 81–177.CrossRefGoogle Scholar
Moeglin, C., Idéaux bilatères des algèbres enveloppantes . Bull. Soc. Math. France 108(1980), 143–186.CrossRefGoogle Scholar
Pink, R. and Roessler, D., On $\psi$ -invariant subvarieties of semiabelian varieties and the Manin–Mumford conjecture . J. Algebraic Geom. 13(2004), no. 4, 771–798.CrossRefGoogle Scholar
Reichstein, Z., Rogalski, D., and Zhang, J. J., Projectively simple rings . Adv. Math. 203(2006), no. 2, 365–407.CrossRefGoogle Scholar
Xie, J., Periodic points of birational transformations on projective surfaces . Duke Math. J. 164(2015), no. 5, 903–932.Google Scholar
Xie, J., The existence of Zariski dense orbits for endomorphisms of projective surfaces (with an appendix in collaboration with T. Tucker), 2019, 66 pp., available online at https://arxiv.org/pdf/1905.07021.pdf Google Scholar
Zhang, S., Distributions in algebraic dynamics , In: Surveys in differential geometry, Vol. X, International Press, Somerville, MA, 2006, pp. 381–430.Google Scholar