Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Asmar, Nakhl
Watson, Saleem
and
Watson, Saleem
1992.
Harmonic conjugation in L1 on compact abelian groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 111,
Issue. 1,
p.
113.
Asmar, Nakhlé H.
and
Montgomery-Smith, Stephen J.
1997.
Hardy Martingales and Jensen's inequality.
Bulletin of the Australian Mathematical Society,
Vol. 55,
Issue. 2,
p.
185.

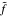 in
in 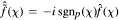 for all
for all 