Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T06:26:03.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Connectedness of the Invertibles in Certain Nest Algebras

Published online by Cambridge University Press:  20 November 2018

Kenneth R. Davidson ,
John Lindsay  and
David R. Pitts
Kenneth R. Davidson
Affiliation:
Pure Mathematics Department, University of Waterloo, Waterloo, Ontario, N2L 3G1, e-mail:krdavids@math.uwaterloo.ca
John Lindsay
Affiliation:
Mathematics Department, University of Nebraska, Lincoln, Nebraska 68588-0323, U.S.A. e-mail:jorr@unlinfo.uni.edu
David R. Pitts
Affiliation:
Mathematics Department, University of Nebraska, Lincoln, Nebraska 68588-0323, U.S.A. e-mail:dpitts@unlinfo2.unl.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

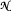We show that if is a nest with no isolated atoms of finite multiplicity, then the invertibles in 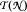are connected. The key technical ingredient is that in such nest algebras, every operator with zero atomic diagonal part factors through the non-atomic part of . In particular, these results apply for the Cantor nest.

Keywords

47D25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 38 , Issue 4 , 01 December 1995 , pp. 412 - 420
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Davidson, K. R., Similarity and compact perturbations of nest algebras, J. Reine Angew. Math. 348(1984), 286–294.Google Scholar
2. Davidson, K. R., Nest Algebras, Pitman Research Notes Math. Ser. 191, Longman Scientific and Technical Pub. Co., London, New York, 1988.Google Scholar
3. Davidson, K. R. and Orr, J. L., Connectedness of the invertibles in infinite multiplicity nest algebras, Bull. London Math. Soc, to appear.Google Scholar
4. Larson, D. R. and Pitts, D. R., Idempotents in nest algebras, J. Funct. Anal. 97(1991), 162–193.Google Scholar
5. Orr, J. L., Triangular algebras and ideals of nest algebras, preprint.Google Scholar
6. Radjavi, H., The group generated by involutions, Proc. Roy. Irish Acad. Sect. A 81(1981), 9–12.Google Scholar
7. Wu, P. Y., The operator factorization problems, Linear Algebra Appl. 117(1989), 35–63.Google Scholar