No CrossRef data available.
Article contents
The Continuous Dependence on the Nonlinearities of Solutions of Fast Diffusion Equations
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, we consider the Cauchy problem
$$\left\{ \begin{align}& {{u}_{t}}=\Delta ({{u}^{m}}),\,\,\,\,\,x\in {{\mathbb{R}}^{N}},t>0,N\ge 3, \\& u(x,0)={{u}_{0}}(x),\,\,\,\,\,x\in {{\mathbb{R}}^{N}}. \\ \end{align} \right.$$
We will prove that
(i) for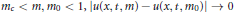 
${{m}_{c}}\,<\,m,\,{{m}_{0}}\,<\,1,\,\left| u(x,\,t,m)-u(x,\,t,{{m}_{0}}) \right|\,\to \,0$ as 
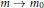$m\,\to \,{{m}_{0}}$ uniformly on every compact subset of 
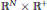${{\mathbb{R}}^{N}}\,\times \,{{\mathbb{R}}^{+}}$ , where 
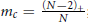${{m}_{c}}\,=\,\frac{{{(N-2)}_{+}}}{N}$ ;
(ii) there is a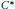 
${{C}^{*}}$ that explicitly depends on 
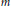$m$ such that
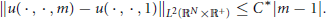$${{\left\| u(\cdot ,\cdot ,m)-u(\cdot ,\cdot ,1) \right\|}_{{{L}^{2}}({{\mathbb{R}}^{N}}\times {{\mathbb{R}}^{+}})}}\le {{C}^{*}}\left| m-1 \right|.$$
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
[1] Aronson, D. G. and Bénilan, P., Régularité des solutions de l’équation des milieux poreux dans ℝ
n.
C. R. Acad. Sci. Paris Sér. A-B
288(1979), no. 2, A103–A105.Google Scholar
[2] Bénilan, P. and Crandall, M. G., The continuous dependence on ϕ of solution of ut– Δϕ(u) = 0.
J. Indiana Univ. Math.
30(1981), no. 2. 161–177. http://dx.doi.org/10.1512/iumj.1981.30.30014
Google Scholar
[3] Cockburn, B. and Gripenberg, G., Continuous dependence on the nonlinearities of solutions of degenerate parabolic equations. J. Differential Equations
151(1999), no. 2, 231–251. http://dx.doi.org/10.1006/jdeq.1998.3499
Google Scholar
[4] Ebmeyer, C., Regularity in Sobolev spaces for the fast diffusion and the porus medium equation. J. Math. Anal. Appl.
307(2005), no. 1, 134–152. http://dx.doi.org/10.1016/j.jmaa.2005.01.009
Google Scholar
[5] Esteban, J. R., Rodriguez, A., and Vázquez, J. L., A nonlinear heat equation with singular diffusivity. Commun. Partial Differential Equations
13(1988), no. 8, 985–1039. http://dx.doi.org/10.1080/03605308808820566
Google Scholar
[6] Gilding, B. H. and Peletier, L. A., The Cauchy problem for an equation in the theory of infiltration. Arch. Rational Mech. Anal.
61(1976), no. 2, 127–140.Google Scholar
[7] Herrero, M. A. and Pierre, M., The Cauchy problem for ut = Δum when 0 < m < 1.
Tran. Amer. Math. Soc.
291(1985), no. 1, 145–158.Google Scholar
[8] Hui, K. M., Existence of solutions of the very fast diffusion equation. Nonlinear Anal.
58(2004), no. 1–2, 75–101. http://dx.doi.org/10.1016/j.na.2004.05.001
Google Scholar
[9] Pan, J. and Gang, L., The linear approach for a nonlinear infiltration equation. European J. Appl. Math.
17(2006), no. 6, 665–675. http://dx.doi.org/10.1017/S095679250700681X
Google Scholar
[10] Vázquez, J. L., Symmetrization and mass comparison for degenerate nonlinear parobolic and related elliptic equations. Adv. Nonlinear Stud.
5(2005), no. 1, 87–131.Google Scholar
[11] Vázquez, J. L., An introduction to the mathematical theory of the porous medium equation. In: Shape optimization and free boundaries (Montreal, PQ, 1990), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., Kluwer Acad. Publ., Dordrecht, 1992, pp. 347–389.Google Scholar
[12] Vázquez, J. L., Smoothing and decay estimates for nonlinear diffusion equations. Equations of porous medium type. Oxford Lecture Series in Mathematics and its Applications, 33, Oxford University Press, Oxford, 2006.Google Scholar
You have
Access