Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T12:37:44.094Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence of Averaged Occupation Times

Published online by Cambridge University Press:  20 November 2018

Charles W. Lamb✝
Charles W. Lamb✝*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X = {Xt, t ≥ 0} be a stationary Markov process with values in a measurable space (S, ℬ), transition function p, and initial distribution concentrated at a point x ∊ S. The occupation times of a set A ∊ ℬ are defined for t ≥ 0 by

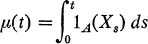
where 1A is the indicator function of A. The expected occupation times are given by

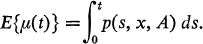
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 1 , April 1975 , pp. 49 - 56
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Breiman, L., Probability (Addison-Wesley, Reading 1968).Google Scholar
2. Brosamler, G. A., The asymptotic behavior of certain additive junctionals of Brownian motion, Inventiones Math., 20 (1973), 87-96.Google Scholar
3. Chung, K. L. and Erdös, P., Probability limit theorems assuming only the first moment I, Memoirs of the Amer. Math. Sac., 6 (1951).Google Scholar
4. Darling, D. A. and Kac, M., On occupation times for Markov processes, Trans. Amer. Math. Soc. 84 (1957), 444-458.Google Scholar
5. Feller, W., An introduction to probability theory and its applications, Volume II (Wiley, New York, 1971).Google Scholar
6. Kallianpur, G. and Robbins, H., Ergodic property of the Brownian motion process, Proc. Nat. Acad. Sci. U.S.A., 39 (1953), 525-533.Google Scholar