Article contents
Convergence of Solutions of Third Order Differential Equations*
Published online by Cambridge University Press: 20 November 2018
Extract
Consider a system of differential equations 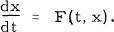 . Solutions of this system are said to be convergent if, given any pair of solutions x(t), y(t), x(t) - y(t) → 0 as t → ∞. In this case the system is also said to be extremely stable.
. Solutions of this system are said to be convergent if, given any pair of solutions x(t), y(t), x(t) - y(t) → 0 as t → ∞. In this case the system is also said to be extremely stable.
In [6] a technique was developed which yielded the convergence of solutions of the forced Lienard equation. Here a similar technique i s applied to forced third order equations. A critical step in [6] was to show that a certain matrix was negative definite. This could be done directly in [6] since the matrix was only 2 × 2. With third and higher order equations, direct use of necessary and sufficient conditions is not feasible since the computations become unwieldy.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1969
Footnotes
This work was supported in part by National Science Foundation COSIP (GY 4754).
Much of this paper is a part of the author's Ph. D. dissertation at the University of Iowa. The author wishes to thank Professor P.E. Waltman for his advice and encouragement.
References
- 2
- Cited by


