Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Djoković, Dragomir Z.
1965.
On the field of a linear transformation.
Archiv der Mathematik,
Vol. 16,
Issue. 1,
p.
371.
Au-Yeung, Yik-Hoi
1975.
A simple proof of the convexity of the field of values defined by two hermitian forms.
Aequationes Mathematicae,
Vol. 12,
Issue. 1,
p.
82.
Goldberg, Moshe
1979.
On certain finite dimensional numerical ranges and numerical radii†.
Linear and Multilinear Algebra,
Vol. 7,
Issue. 4,
p.
329.
Marcus, Marvin
1979.
SOME COMBINATORIAL ASPECTS OF NUMERICAL RANGE*.
Annals of the New York Academy of Sciences,
Vol. 319,
Issue. 1,
p.
368.
Marcus, Marvin
and
Sandy, Markus
1985.
Conditions for the generalized numerical range to be real.
Linear Algebra and its Applications,
Vol. 71,
Issue. ,
p.
219.
Grone, Robert
1994.
A biography of Marvin Marcus.
Linear Algebra and its Applications,
Vol. 201,
Issue. ,
p.
1.


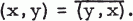 In U
In U