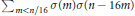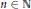Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alaca, Şaban
and
Williams, Kenneth S.
2010.
The number of representations of a positive integer by certain octonary quadratic forms.
Functiones et Approximatio Commentarii Mathematici,
Vol. 43,
Issue. 1,
ALACA, AYŞE
ALACA, ŞABAN
and
WILLIAMS, KENNETH S.
2010.
FOURTEEN OCTONARY QUADRATIC FORMS.
International Journal of Number Theory,
Vol. 06,
Issue. 01,
p.
37.
Xia, Ernest X. W.
Yao, Olivia X. M.
and
Hartung, Ferenc
2012.
Eisenstein Series Identities Involving the Borweins′ Cubic Theta Functions.
Journal of Applied Mathematics,
Vol. 2012,
Issue. 1,
Kim, Dae-Yeoul
Kim, Ae-Ran
and
Park, Hwa-Sin
2012.
ONVOLUTION SUM Σm<n/8σ1(2m)σ1(n-8m).
Honam Mathematical Journal,
Vol. 34,
Issue. 1,
p.
63.
RAMAKRISHNAN, B.
and
SAHU, BRUNDABAN
2013.
EVALUATION OF THE CONVOLUTION SUMS ∑l+15m=nσ(l)σ(m) AND ∑3l+5m=nσ(l)σ(m) AND AN APPLICATION.
International Journal of Number Theory,
Vol. 09,
Issue. 03,
p.
799.
Cho, Bumkyu
Kim, Daeyeoul
and
Park, Ho
2013.
Evaluation of a certain combinatorial convolution sum in higher level cases.
Journal of Mathematical Analysis and Applications,
Vol. 406,
Issue. 1,
p.
203.
Kim, Daeyeoul
2013.
CONVOLUTION SUMS OF ODD AND EVEN DIVISOR FUNCTIONS.
Honam Mathematical Journal,
Vol. 35,
Issue. 3,
p.
445.
Kim, Aeran
Kim, Daeyeoul
and
Yan, Li
2013.
CONVOLUTION SUMS ARISING FROM DIVISOR FUNCTIONS.
Journal of the Korean Mathematical Society,
Vol. 50,
Issue. 2,
p.
331.
Lee, Kwangchul
Kim, Daeyeoul
and
Seo, Gyeong-Sig
2014.
A REMARK OF ODD DIVISOR FUNCTIONS AND WEIERSTRASS ℘-FUNCTIONS.
Honam Mathematical Journal,
Vol. 36,
Issue. 1,
p.
55.
Ramakrishnan, B.
and
Sahu, Brundaban
2014.
On the number of representations of an integer by certain quadratic forms in sixteen variables.
International Journal of Number Theory,
Vol. 10,
Issue. 08,
p.
1929.
Cooper, Shaun
and
Ye, Dongxi
2014.
Evaluation of the convolution sums ∑l+20m=n σ(l)σ(m), ∑4l+5m=n σ(l)σ(m) and ∑2l+5m=n σ(l)σ(m).
International Journal of Number Theory,
Vol. 10,
Issue. 06,
p.
1385.
Xia, Ernest X. W.
Tian, X. L.
and
Yao, Olivia X. M.
2014.
Evaluation of the convolution sum ∑i+25j=n σ(i)σ(j).
International Journal of Number Theory,
Vol. 10,
Issue. 06,
p.
1421.
Kim, Aeran
Kim, Daeyeoul
and
Sankaranarayanan, Ayyadurai
2014.
ARITHMETIC SUMS SUBJECT TO LINEAR AND CONGRUENT CONDITIONS AND SOME APPLICATIONS.
Honam Mathematical Journal,
Vol. 36,
Issue. 2,
p.
305.
Ye, Dongxi
2015.
Evaluation of the convolution sums ∑l+36m=n σ(l)σ(m) and ∑4l+9m=n σ(l)σ(m).
International Journal of Number Theory,
Vol. 11,
Issue. 01,
p.
171.
Alaca, Şaban
and
Kesicioğlu, Yavuz
2016.
Evaluation of the convolution sums ∑l+27m=nσ(l)σ(m) and ∑l+32m=nσ(l)σ(m).
International Journal of Number Theory,
Vol. 12,
Issue. 01,
p.
1.
Lee, Kwangchul
Kim, Daeyeoul
and
Seo, Gyeong-Sig
2016.
A PRODUCT FORMULA FOR COMBINATORIC CONVOLUTION SUMS OF ODD DIVISOR FUNCTIONS.
Honam Mathematical Journal,
Vol. 38,
Issue. 2,
p.
243.
Park, Yoon Kyung
2016.
Evaluation of the convolution sums ∑++=σ(k)σ(l)σ(m) with lcm(a,b,c)≤6.
Journal of Number Theory,
Vol. 168,
Issue. ,
p.
257.
Park, Yoon Kyung
2017.
Evaluation of the convolution sums ∑al+bm=n lσ(l) σ(m) with ab ≤ 9.
Open Mathematics,
Vol. 15,
Issue. 1,
p.
1389.
Köklüce, Bülent
and
Eser, Hasan
2017.
Evaluation of some convolution sums and representation of integers by certain quadratic forms in 12 variables.
International Journal of Number Theory,
Vol. 13,
Issue. 03,
p.
775.
Lee, Joohee
and
Park, Yoon Kyung
2017.
Evaluation of the convolution sums ∑a1m1+a2m2+a3m3+a4m4=nσ(m1)σ(m2)σ(m3)σ(m4) with lcm(a1,a2,a3,a4) ≤ 4.
International Journal of Number Theory,
Vol. 13,
Issue. 08,
p.
2155.