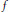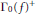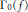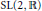Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
HORI, Yasuto
HIRANO, Yuichiro
TACHIBANA, Satoshi
YAMANE, Masanobu
SHIMASE, Takuya
AMANO, Tomomasa
and
KOMAKI, Takaaki
2010.
Wood Preservation,
Vol. 36,
Issue. 5,
p.
192.
PAZ, B. E. R.
VELLOSO, C. C. V.
JÚNIOR, E. N. O.
COIMBRA, J. S. R.
and
SANTOS, I. J. B.
2017.
OBTENÇÃO E CARACTERIZAÇÃO DE NANOESTRUTURAS DE CARBONATO DE CÁLCIO.
p.
710.
Bajpai, Jitendra
2019.
Lifting of Modular Forms.
Publications mathématiques de Besançon. Algèbre et théorie des nombres,
p.
5.