Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T17:21:22.062Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclicity in Dirichlet Spaces

Part of: Special classes of linear operators Geometric function theory Spaces and algebras of analytic functions

Published online by Cambridge University Press:  11 January 2019

Y. Elmadani  and
I. Labghail
Y. Elmadani
Affiliation:
CeReMAR LAMA, Mohammed V University, Faculty of science Rabat, 10 000 Rabat, Morocco Email: elmadanima@gmail.comimaneayaa@gmail.com
I. Labghail
Affiliation:
CeReMAR LAMA, Mohammed V University, Faculty of science Rabat, 10 000 Rabat, Morocco Email: elmadanima@gmail.comimaneayaa@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\unicode[STIX]{x1D707}$ be a positive finite Borel measure on the unit circle and 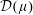${\mathcal{D}}(\unicode[STIX]{x1D707})$ the associated harmonically weighted Dirichlet space. In this paper we show that for each closed subset 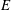$E$ of the unit circle with zero 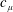$c_{\unicode[STIX]{x1D707}}$-capacity, there exists a function $f\in {\mathcal{D}}(\unicode[STIX]{x1D707})$ such that 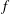$f$ is cyclic (i.e., 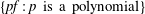$\{pf:p\text{ is a polynomial}\}$ is dense in 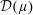${\mathcal{D}}(\unicode[STIX]{x1D707})$), 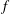$f$ vanishes on 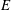$E$, and 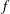$f$ is uniformly continuous. Next, we provide a sufficient condition for a continuous function on the closed unit disk to be cyclic in 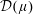${\mathcal{D}}(\unicode[STIX]{x1D707})$.

Keywords

Dirichlet-type spacecyclic vectorcapacitystrong-type inequality

MSC classification

Primary: 47B38: Operators on function spaces (general)
Secondary: 30C85: Capacity and harmonic measure in the complex plane 30H05: Bounded analytic functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 247 - 257
Copyright
© Canadian Mathematical Society 2019 

References

Beurling, A., On two problems concerning linear operators in Hilbert space . Acta Math. 81(1948), 239–255. https://doi.org/10.1007/BF02395019.Google Scholar
Brown, L. and Cohn, W., Some examples of cyclic vectors in the Dirichlet space . Proc. Amer. Math. Soc. 95(1985), 42–46. https://doi.org/10.2307/2045570.Google Scholar
Brown, L. and Shields, A., Cyclic vectors in the Dirichlet space . Trans. Amer. Math. Soc. 285(1984), 269–304. https://doi.org/10.2307/1999483.Google Scholar
Carleson, L., Sets of uniqueness for functions regular in the unit circle . Acta Math. 87(1952), 325–345. https://doi.org/10.1007/BF02392289.Google Scholar
Chacón, G., Carleson measures on Dirichlet-type spaces . Proc. Amer. Math. Soc. 139(2011), 1605–1615. https://doi.org/10.1090/S0002-9939-2011-10823-2.Google Scholar
Chartrand, R., Toeplitz operators on Dirichlet-type spaces . J. Operator Theory. 48(2002), 3–13.Google Scholar
El-Fallah, O., Elmadani, Y., and Kellay, K., Kernel estimate and capacity in the Dirichlet spaces . J. Funct. Anal., to appear. https://doi.org/10.1016/j.jfa.2018.03.017.Google Scholar
El-Fallah, O., Elmadani, Y., and Kellay, K., Cyclicity and invariant subspaces in Dirichlet spaces . J. Funct. Anal. 270(2016), 3262–3279. https://doi.org/10.1016/j.jfa.2016.02.027.Google Scholar
El-Fallah, O., Kellay, K., Mashreghi, J., and Ransford, T., A primer on the Dirichlet space. Cambridge Tracts in Mathematics, 203, Cambridge University Press, Cambridge, 2014.Google Scholar
El-Fallah, O., Kellay, K., and Ransford, T., Cyclicity in the Dirichlet space. Ark. Mat. 44 (2006), 61–86. https://doi.org/10.1007/s11512-005-0008-z.Google Scholar
El-Fallah, O., Kellay, K., and Ransford, T., On the Brown-Shields conjecture for cyclicity in the Dirichlet space. Adv. Math. 222(2009), no. 6, 2196–2214. https://doi.org/10.1016/j.aim.2009.07.011.Google Scholar
El-Fallah, O., Kellay, K., and Ransford, T., Cantor sets and cyclicity in weighted Dirichlet spaces . J. Math. Anal. Appl. 372(2010), 565–573. https://doi.org/10.1016/j.jmaa.2010.07.047.Google Scholar
Fukushima, M., Oshima, Y., and Takeda, M., Dirichlet forms and symmetric Markov processes. Second revised and extended ed., de Gruyter Studies in Mathematics, 19, Walter de Gruyter & Co., Berlin, 2011.Google Scholar
Guillot, D., Comportement au bord dans les espaces de Dirichlet avec poids harmoniques et espaces de de Branges-Rovnyak. PhD thesis, Universite Laval, 2010.Google Scholar
Guillot, D., Fine boundary behavior and invariant subspaces of harmonically weighted Dirichlet spaces. Complex Anal. Oper. Theory. 6(2012), 1211–1230. https://doi.org/10.1007/s11785-010-0124-z.Google Scholar
Hedenmalm, H. and Shields, A., Invariant subspaces in Banach spaces of analytic functions . Michigan Math. J. 37(1990), no. 1, 91–104. https://doi.org/10.1307/mmj/1029004068.Google Scholar
Meyers, N. G., A theory of capacities for potentials of functions in lebesgue classes . Math. Scand. 26(1971), 255–292. https://doi.org/10.7146/math.scand.a-10981.Google Scholar
Richter, S., A representation theorem for cyclic analytic two-isometries . Trans. Amer. Math. Soc. 328(1991), 325–349. https://doi.org/10.2307/2001885.Google Scholar
Richter, S. and Sundberg, C., Multipliers and invariant subspaces in the Dirichlet space . J. Operator Theory 28(1992), 167–186.Google Scholar
Shimorin, S. M., Reproducing kernels and extremal functions in Dirichlet-type spaces . J. Math. Sci. (N.Y.) 107(2001), 4108–4124. https://doi.org/10.1023/A:1012453003423.Google Scholar