Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T08:02:27.352Z Has data issue: false hasContentIssue false
  • English
  • Français

Decompositions of Localized Fibres and Cofibres

Published online by Cambridge University Press:  20 November 2018

John Oprea
John Oprea*
Affiliation:
Cleveland State UniversityCleveland, Ohio44115
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper p-local versions of the Rational Fibre and Cofibre Decomposition Theorems are given. In particular, if there exists an element in the nth Gottlieb group of a space F such that its image under the Hurewicz map has infinite order, then 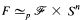Sn for almost all primes p. A dual result is proved for cofibrations.

Keywords

55P9955P60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 4 , 01 December 1988 , pp. 424 - 431
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Cartan, H., La transgression dans un groupe de Lie et dans un espace fibre principal Colloque de Topologie, Bruxelles 1950, pp. 57–71.Google Scholar
2. Felix, Y. and Halperin, S., Rational L.S. category and its applications TAMS, 273 no. 1 (1982), pp. 1–36.Google Scholar
3. Felix, Y. and Lemaire, J. M., On the mapping theorem for Lusternik-Schnirelman category Topology 24 no. 1 (1985), pp. 41–43.Google Scholar
4. Gottlieb, D., Evaluation subgroups of homotopy groups Amer. J. Math. 91 (1969), pp. 729–756.Google Scholar
5. Gottlieb, D., The evaluation map and homology Mich. Math. J. 19 (1972), pp. 289–297.Google Scholar
6. Gottlieb, D., Witnesses, transgressions and the evaluation map Ind. Math. J. 24 no. 9 (1975), pp. 825–836.Google Scholar
7. Hilton, P., Homotopy theory and duality Gordon and Breach, New York, 1965.Google Scholar
8. Hilton, P., Mislin, G. and Roitberg, J., Localization of nilpotent groups and spaces North Holland, Amsterdam, 1975.Google Scholar
9. McGibbon, C A. and Wilkerson, C., Loop spaces affinité complexes at large primes Proc. AMS 96 no. 4(1986), pp. 698–702.Google Scholar
10. Oprea, J., Decomposition theorems in rational homotopy theory Proc. AMS 96 no. 3 (1986), pp. 505–512.Google Scholar
11. Oprea, J., The Samelson space of a fibration Mich. Math. J. 34 (1987), pp. 127–141.Google Scholar
12. Oprea, J., A homotopical Conner-Raymond theorem preprint, Cleveland State University, 1987.Google Scholar
13. Sullivan, D., Geometric topology, part I: Localization, periodicity and Galois symmetry MIT 1970 (mimeographed notes).Google Scholar