Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T12:44:07.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Degeneracy of 2-Forms and 3-Forms

Published online by Cambridge University Press:  20 November 2018

L. M. Fehér ,
A. Némethi  and
R. Rimányi
L. M. Fehér
Affiliation:
Department of Analysis, Eotvos University, Budapest, Hungary e-mail: lfeher@math-inst.hu
A. Némethi
Affiliation:
Department of Mathematics, The Ohio State University e-mail: nemethi@math.ohio-state.edu
R. Rimányi
Affiliation:
Department of Mathematics, University of North Carolina at Chapel Hill e-mail: rimanyi@email.unc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study some global aspects of differential complex 2-forms and 3-forms on complex manifolds. We compute the cohomology classes represented by the sets of points on a manifold where such a form degenerates in various senses, together with other similar cohomological obstructions. Based on these results and a formula for projective representations, we calculate the degree of the projectivization of certain orbits of the representation 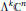${{\Lambda }^{k}}{{\mathbb{C}}^{n}}$

Keywords

14N1057R45Classes of degeneracy loci2-forms3-formsThom polynomialsglobal singularity Theory
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 4 , 01 December 2005 , pp. 547 - 560
Copyright
Copyright © Canadian Mathematical Society 2005

References

[AB83] Atiyah, M. and Bott, R., The Yang-Mills equation over Riemann surfaces. Philos. Trans. Roy. Soc. London Ser. A 308(1983), 523–615.Google Scholar
[CDP80] Eisenbud, D., De Concini, C., and Procesi, C., Young diagrams and determinantal varieties. Invent.Math. 56(1980), 129–165.Google Scholar
[Don77] Donagi, R. Y, On the geometry of Grassmannians. Duke Math. J. 44(1977), 795–837.Google Scholar
[FR] Fehér, L. and Rimányi, R., Calulation of Thom polynomials and other cohomological obstructions for group actions. To appear in Contemp. Math. AMS; avaliable at http://www.unc.edu/rimanyi/cikkek Google Scholar
[Ful98] Fulton, W., Intersection Theory. Second edition. Ergebnisse der mathematik und ihrer Grenzgebiete 3, Springer-Verlag, Berlin, 1998.Google Scholar
[FH91] Fulton, W. and Harris, J., Representation Theory. A First Course. Graduate Texts in Mathematics 129, Springer-Verlag, New York, 1991.Google Scholar
[FP98] Fulton, W. and Pragacz, P., Schubert varieties and degeneracy loci. Lecture Notes in Mathematics 1689, Springer-Verlag, Berlin, 1998.Google Scholar
[GS] Grayson, D. R. and Stillman, M. E., Macaulay 2, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2.Google Scholar
[HT84] Harris, J. and Tu, L. W., On symmetric and skew-symmetric determinantal varieties. Topology 23(1984), 71–84.Google Scholar
[Her83] Herz, C., Alternating 3-forms and exceptional simple Lie groups of type G 2 . Canad. J. Math. 35(1983), 776–806.Google Scholar
[Hit00] Hitchin, N., The geometry of three-forms in six dimensions. J. Differential Geom. 55(2000), 547–576.Google Scholar
[Hit01] Hitchin, N., Stable forms and special metrics. In: Global Differential Geometry: The Mathematical Legacy of Alfred Gray, Contemp. Math. 288, Amer.Math. Soc., Providence, RI, 2001, pp. 70–89.Google Scholar
[Hol79] Holme, A., On the dual of a smooth variety. In: Algebraic Geometry, Lecture Notes in Math. 732, Springer, Berlin, 1979, pp. 144–156.Google Scholar
[JLP81] Józefiak, T., Lascoux, A., and Pragacz, P., Classes of determinantal varieties associated with symmetric and antisymmetris matrices. Izv. Akad. Nauk SSSR Ser. Mat. 45(1981), 662–673.Google Scholar
[Joy] Joyce, D. D., Constructing compact manifolds with exceptional holonomy. DG/0203158.Google Scholar
[Joy00] Joyce, D. D., Compact manifolds with special holonomy. Oxford Mathematical Monographs, Oxford University Press, 2000.Google Scholar
[Kaz97] Kazarian, M. É., Characteristic classes of singularity theory. In: The Arnold-Gelfand Mathematical Seminars, Birkhäuser Boston, Boston, MA, 1997, pp. 325–340.Google Scholar
[Las81] Lascoux, A., Degree of the dual of a Grassman variety. Comm. Algebra 9(1981), 1215–1225.Google Scholar
[Pra88] Pragacz, P., Enumerative geometry of degeneracy loci. Ann. Sci. école Norm. Sup. (4) 21(1988), 413–454.Google Scholar
[Pra90] Pragacz, P., Cycles of isotropic subspaces and formulas for symmetric degeneracy loci. In: Topics in Algebra, II, Banach Center Publ. 26, Warsaw, 1990, pp. 189–199.Google Scholar
[PR96] Pragacz, P. and Ratajski, J., Polynomials homologically supported on degeneracy loci. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 23(1996), 99–118.Google Scholar
[SS99] Saeki, O. and Sakuma, K., Elimination of singularities: Thom polynomial and beyond. In: Singularity Theory, LondonMath. Soc. Lect Note Ser. 263, Cambridge, Cambridge University Press, 1999, pp. 291–304.Google Scholar