Degree Homogeneous Subgroups

Abstract

Let $G$ be a finite group and 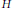$H$ be a subgroup. We say that 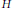$H$ is degree homogeneous if, for each $x\,\in \,\text{Irr}\left( G \right)$, all the irreducible constituents of the restriction 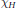${{x}_{H}}$ have the same degree. Subgroups which are either normal or abelian are obvious examples of degree homogeneous subgroups. Following a question by E.M. Zhmud’, we investigate general properties of such subgroups. It appears unlikely that degree homogeneous subgroups can be characterized entirely by abstract group properties, but we providemixed criteria (involving both group structure and character properties) which are both necessary and sufficient. For example, 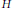$H$ is degree homogeneous in $G$ if and only if the derived subgroup 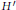${H}'$ is normal in $G$ and, for every pair $\alpha $, 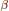$\beta $ of irreducible $G$-conjugate characters of 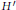${H}'$, all irreducible constituents of 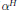${{\alpha }^{H}}$ and 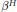${{\beta }^{H}}$ have the same degree.