Article contents
The Densest Packing of Six Spheres in a Cube
Published online by Cambridge University Press: 20 November 2018
Extract
This packing problem is obviously equivalent to the problem of locating six points Pi(l ≤ i ≤ 6) in a- closed unit cube C such that 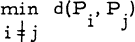 is as large as possible, where d(Pi, Pj) denotes the distance between Pi and Pj. We shall prove that this minimum distance cannot exceed
is as large as possible, where d(Pi, Pj) denotes the distance between Pi and Pj. We shall prove that this minimum distance cannot exceed 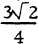 (= m, say), and that 4 it attains this value only if the points form a configuration which is congruent to the one of the points Ri(l≤i≤6) shown in fig. 1. Note that
(= m, say), and that 4 it attains this value only if the points form a configuration which is congruent to the one of the points Ri(l≤i≤6) shown in fig. 1. Note that 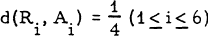 , and so the six points are the vertices of a regular octahedron.
, and so the six points are the vertices of a regular octahedron.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1966
References
- 6
- Cited by


