Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T19:26:27.751Z Has data issue: false hasContentIssue false
  • English
  • Français

Density of Non Quasi-Analytic Classes of Functions

Published online by Cambridge University Press:  20 November 2018

Thu Pham-Gia
Thu Pham-Gia*
Affiliation:
Département de Mathématiques, Université de Moncton, Moncton, N.-B. Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the study of quasi-analytic classes (see [3], pp. 372-379), a class C{Mn} is shown to have the following properties:

  1. (a) If M0= 1 and 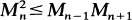(i.e. {Mn} is log convex), C{Mn} forms an algebra.

  2. (b) C{Mn} is invariant under affine transformations.

  3. (c) C{Mn} is quasi-analytic iff it contains non non-trivial function with compact support.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 4 , 01 December 1977 , pp. 467 - 469
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Lelong, P., Extension d'un théorème de Car?eman, Ann. Inst. Fourier, Grenoble, 12 (1962), 627-641.Google Scholar
2. Ronkin, L.I., Quasi-analytic classes of functions of several variables, Soviet Math. Dokl. 3, 146 (1962), 1360-1363.Google Scholar
3. Rudin, W., Real and complex analysis, McGraw-Hill, New York, 1966.Google Scholar