Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T08:52:55.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Density of Polynomial Maps

Published online by Cambridge University Press:  20 November 2018

Chen-Lian Chuang  and
Tsiu-Kwen Lee
Chen-Lian Chuang
Affiliation:
Department of Mathematics, National Taiwan University, Taipei 106, Taiwan e-mail: chuang@math.ntu.edu.tw e-mail: tklee@math.ntu.edu.tw
Tsiu-Kwen Lee
Affiliation:
Department of Mathematics, National Taiwan University, Taipei 106, Taiwan e-mail: chuang@math.ntu.edu.tw e-mail: tklee@math.ntu.edu.tw
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 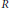$R$ be a dense subring of $\text{End}\left( _{D}V \right)$, where 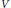$V$ is a left vector space over a division ring 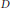$D$. If 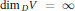$\dim{{\,}_{D}}V\,=\,\infty $, then the range of any nonzero polynomial 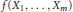$f\left( {{X}_{1}},\,\ldots \,,\,{{X}_{m}} \right)$ on 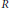$R$ is dense in $\text{End}\left( _{D}V \right)$. As an application, let 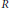$R$ be a prime ring without nonzero nil one-sided ideals and 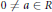$0\,\ne \,a\,\in \,R$. If 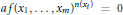$af{{\left( {{x}_{1}},\ldots ,{{x}_{m}} \right)}^{n\left( {{x}_{i}} \right)}}\,=\,0$ for all 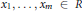${{x}_{1}},\,\ldots \,,\,{{x}_{m}}\,\in \,R$, where 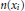$n\left( {{x}_{i}} \right)$ is a positive integer depending on 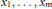${{x}_{1}},\,\ldots \,,\,{{x}_{m}}\,\in \,R$, then 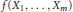$f\left( {{X}_{1}},\,\ldots \,,\,{{X}_{m}} \right)$ is a polynomial identity of 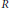$R$ unless 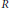$R$ is a finite matrix ring over a finite field.

Keywords

16D6016S50densitypolynomialendomorphism ringPI
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 223 - 229
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Beidar, K. I., Martindale, W. S. III, and Mikhalev, A. V., Rings with Generalized Identities. Monographs and Textbooks in Pure and Applied Mathematics 196. Marcel Dekker, New York, 1996.Google Scholar
[2] Chuang, C.-L., On nilpotent derivations of prime rings. Proc. Amer. Math. Soc. 107(1989), no. 1, 67–71. doi:10.2307/2048036Google Scholar
[3] Chuang, C.-L., On ranges of polynomials in finite matrix rings. Proc. Amer. Math. Soc. 110(1990), no. 2, 293–302. doi:10.2307/2048069Google Scholar
[4] Chuang, C.-L. and Lee, T.-K., Rings with annihilator conditions on multilinear polynomials. Chinese J. Math. 24(1996), no. 2, 177–185.Google Scholar
[5] Faith, C. and Utumi, Y., On a new proof of Litoff 's theorem. Acta Math. Acad. Sci. Hungar 14(1963), 369–371. doi:10.1007/BF01895723Google Scholar
[6] Felzenszwalb, B., On a result of Levitzki. Canad. Math. Bull. 21(2) (1978), 241–242.Google Scholar
[7] Felzenszwalb, B. and Giambruno, A., Periodic and nil polynomials in rings. Canad. Math. Bull. 23(1980), no. 4, 473–476.Google Scholar
[8] Lee, T.-K., Derivations and centralizing mappings in prime rings. Taiwanese J. Math. 1(1997), no. 3, 333–342.Google Scholar
[9] Martindale, W. S. III, Prime rings satisfying a generalized polynomial identity. J. Algebra 12(1969), 576–584. doi:10.1016/0021-8693(69)90029-5Google Scholar
[10] Wong, T.-L., Derivations with power central values on multilinear polynomials. Algebra Colloq. 3(1996), no. 4, 369–378.Google Scholar
[11] Yeh, C.-T. and Chuang, C.-L., Nil polynomials of prime rings. J. Algebra 186(1996), no. 3, 781–792. doi:10.1006/jabr.1996.0394Google Scholar