Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Currie, Melvin R.
1985.
A metric characterization of the irrationals via a group operation.
Topology and its Applications,
Vol. 21,
Issue. 3,
p.
223.

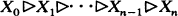 such that dim X
such that dim X