Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T22:41:52.956Z Has data issue: false hasContentIssue false
  • English
  • Français

Discreteness For the Set of Complex Structures On a Real Variety

Published online by Cambridge University Press:  20 November 2018

E. Ballico
E. Ballico*
Affiliation:
Department of Mathematics University of Trento 38050 Povo (TN) Italy, e-mail: ballico@science.unitn.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 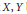$X,\,Y$ be reduced and irreducible compact complex spaces and 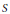$S$ the set of all isomorphism classes of reduced and irreducible compact complex spaces 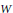$W$ such that 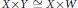$X\,\times \,Y\,\cong \,X\,\times \,W$. Here we prove that 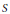$S$ is at most countable. We apply this result to show that for every reduced and irreducible compact complex space $X$ the set 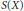$S(X)$ of all complex reduced compact complex spaces 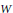$W$ with 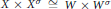$X\,\times \,{{X}^{\sigma }}\,\cong \,W\,\times \,{{W}^{\sigma }}$ (where 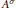${{A}^{\sigma }}$ denotes the complex conjugate of any variety 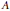$A$) is at most countable.

Keywords

32J1814J9914P99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 3 , 01 September 2003 , pp. 321 - 322
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bochnak, J. and Huisman, J., When is a complex elliptic curve the product of two real algebraic curves? Math. Ann. 293 (1992), 469–474.Google Scholar
[2] Brun, J., Sur la simplification dans les isomorphismes analytiques. Ann. Sci. École Norm. Sup. (4) 9 (1976), 533–538.Google Scholar
[3] Brun, J., Sur la simplification par les variétés homogenes. Math. Ann. 230 (1977), 175–182.Google Scholar
[4] Fujiki, A., Countability of the Douady space of a complex space. Japan. J. Math. (N.S.) 5 (1979), 431–447.Google Scholar
[5] Grothendieck, A., Fondements de la géométrie algébrique. extraits du Séminaire Bourbaki 1957–1962.Google Scholar
[6] Horst, C., Decomposition of compact complex varieties and the cancellation problem. Math. Ann. 271 (1985), 467–477.Google Scholar
[7] Huisman, J., The underlying real algebraic structure of complex elliptic curves. Math. Ann. 294 (1992), 19–35.Google Scholar
[8] Parigi, G., Sur la simplification par les tores complexes. J. Reine Angew.Math. 322 (1981), 42–52.Google Scholar
[9] Parigi, G., Caracterization des variétés compactes simplifiables et applications aux surfaces algébriques. Math. Z. 190 (1985), 371–378.Google Scholar
[10] Silhol, R., Real Algebraic Surfaces. Lecture Notes in Math. 1392, Springer-Verlag, Berlin, Heidelberg, New York, 1986.Google Scholar
[11] Weil, A., Adeles and algebraic groups. Progress in Math. 23, Birkhäuser, Boston, Basel, Stuttgart, 1982.Google Scholar