Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Boyd, David W.
1973.
The residual set dimension of the Apollonian packing.
Mathematika,
Vol. 20,
Issue. 2,
p.
170.
Tóth, G. Fejes
1983.
Convexity and Its Applications.
p.
318.
Tricot, Claude
1989.
Porous surfaces.
Constructive Approximation,
Vol. 5,
Issue. 1,
p.
117.
Tricot, Claude
1989.
Constructive Approximation.
p.
117.
Parker, John R.
1995.
Kleinian circle packings.
Topology,
Vol. 34,
Issue. 3,
p.
489.

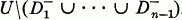 (S
(S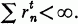 In the sequel we refer to a complete packing simply as a packing.
In the sequel we refer to a complete packing simply as a packing.