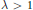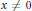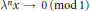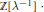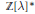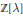Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baker, Veronica
Barge, Marcy
and
Kwapisz, Jaroslaw
2006.
Geometric realization and coincidence for reducible non-unimodular Pisot tiling spaces with an application to β-shifts.
Annales de l'Institut Fourier,
Vol. 56,
Issue. 7,
p.
2213.
Bufetov, Alexander I.
Marshall‐Maldonado, Juan
and
Solomyak, Boris
2025.
Local spectral estimates and quantitative weak mixing for substitution Z${\mathbb {Z}}$‐actions.
Journal of the London Mathematical Society,
Vol. 111,
Issue. 4,